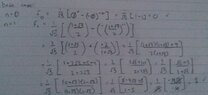Generalized mathematical induction

[Dog1]

Recall that the fibonacci sequence is defined as

{ f₀=0; f₁ = 1 and
{f_n = f _n - 1 + f_n -2 for n 2

Prove by generalized mathematical induction that

f_n = 1/sqrt(5)[ϕⁿ - (-ϕ)^-n]

where ϕ = [1+sqrt(5)]/2

is the golden ratio.. (This is known as de Moivre's formula.)
So I'm completely lost as to how I should start this and I need someone to point me in the right direction. Thanks.

 

[MarkFL]

First, you want to demonstrate that the base case $P_0$ is true:

$$F_0=\frac{1}{\sqrt{5}}\left(\phi^{0}-\phi^{-0} \right)=0$$

Is this true?

Next, state the induction hypothesis:

$$F_k=\frac{1}{\sqrt{5}}\left(\phi^{k}-(-\phi)^{-k} \right)$$

As your inductive step, the recursive definition of the sequence will be helpful. During this process you will want to demonstrate that:

$$\phi^{k}+\phi^{k-1}=\phi^{k+1}$$

and

$$(-\phi)^{-k}+(-\phi)^{-(k-1)}=(-\phi)^{-(k+1)}$$

 

[Evgeny.Makarov]

Hi, and welcome to the forum. Please see the section on strong induction in Wikipedia and possibly other sections of that article.

 

[Dog1]

First, you want to demonstrate that the base case $P_0$ is true:

$$F_0=\frac{1}{\sqrt{5}}\left(\phi^{0}-\phi^{-0} \right)=0$$

Is this true?

Next, state the induction hypothesis:

$$F_k=\frac{1}{\sqrt{5}}\left(\phi^{k}-\phi^{-k} \right)$$

As your inductive step, the recursive definition of the sequence will be helpful. During this process you will want to demonstrate that:

$$\phi^{k}+\phi^{k-1}=\phi^{k+1}$$

and

$$\phi^{-k}+\phi^{-(k-1)}=\phi^{-(k+1)}$$

So my base cases check to be true. I've attached my work here.

View attachment 1849

And fn is true for n. But I'm not sure how to prove for n + 1.

f_n+1= f_(n+1)-1 + f_(n+1)-2

=f_n+f_(n-1)
=1/sqrt(5)[ϕⁿ+ϕ^-n] + 1/sqrt(5) [ϕ^(n-1) ϕ^-(n-1)

What do I do next? If I'm even going in the right direction.

 

[MarkFL]

While it didn't hurt to show it is true for $n=1$, you really only need to show it is true for one case, and demonstration that it is true for $n=0$ is simpler.

Okay, next you want to state the induction hypothesis $P_k$:

$$F_k=\frac{1}{\sqrt{5}}\left(\phi^{k}-(-\phi)^{-k} \right)$$

Now, I suggest adding to this $P_{k-1}$

$$F_{k-1}=\frac{1}{\sqrt{5}}\left(\phi^{k-1}-(-\phi)^{-(k-1)} \right)$$

Aided by the recursion:

$$F_{k+1}=F_{k}+F_{k-1}$$

the left side immediately becomes what you need. And the right side also becomes what you need if you prove the two properties involving $\phi$ I listed in my first post are true.

 

[Evgeny.Makarov]

$$F_k=\frac{1}{\sqrt{5}}\left(\phi^{k}-\phi^{-k} \right)$$

This should say
\[
F_k=\frac{1}{\sqrt{5}}\left(\phi^{k}-(-\phi)^{-k} \right)
\]
just as the original post says.

While it didn't hurt to show it is true for $n=1$, you really only need to show it is true for one case

Hmm...

Okay, next you want to state the induction hypothesis $P_k$:

$$F_k=\frac{1}{\sqrt{5}}\left(\phi^{k}-\phi^{-k} \right)$$

Now, I suggest adding to this $P_{k-1}$

$$F_{k-1}=\frac{1}{\sqrt{5}}\left(\phi^{k-1}-\phi^{-(k-1)} \right)$$

Let's set $k=1$. We have proved $P_0$, but what about $P_1$?

 

[MarkFL]

This should say
\[
F_k=\frac{1}{\sqrt{5}}\left(\phi^{k}-(-\phi)^{-k} \right)
\]
just as the original post says.

Hmm...

Let's set $k=1$. We have proved $P_0$, but what about $P_1$?

I fixed my posts to correctly state the hypothesis. My mistake also that both given initial values need to be shown are true.

 

[MarkFL]

As as aside, we can derive the required result. If we write the recursion as the linear homogeneous difference equation:

$$F_{n}-F_{n-1}-F_{n-2}=0$$

We then find the associated characteristic equation is:

$$r^2-r-1=0$$

Application of the quadratic formula yields the characteristic roots:

$$r=\frac{-(-1)\pm\sqrt{(-1)^2-4(1)(-1)}}{2(1)}=\frac{1\pm\sqrt{5}}{2}$$

Now, if we define:

$$\phi=\frac{1+\sqrt{5}}{2}$$

We then see that:

$$\frac{1-\sqrt{5}}{2}\cdot\frac{1+\sqrt{5}}{1+\sqrt{5}}= \frac{1-5}{2\left(1+\sqrt{5} \right)}=- \frac{2}{1+\sqrt{5}}=(-\phi)^{-1}$$

Hence the characteristic roots may be given as:

$$r=\phi,\,(-\phi)^{-1}$$

And thus, we know the closed form for $F_n$ is given by:

$$F_n=A\phi^n+B(-\phi)^{-n}$$

Now, using the initial values of the sequence, we may determine the values of the parameters $A$ and $B$:

$$F_0=A\phi^0+B(-\phi)^{-0}=A+B=0\implies B=-A$$

$$F_1=A\phi^1+B(-\phi)^{-1}=A\frac{1+\sqrt{5}}{2}-A\frac{1-\sqrt{5}}{2}=A\sqrt{5}=1\implies A=\frac{1}{\sqrt{5}}$$

Hence, we find the solution satisfying the difference equation and the initial values is:

$$F_n=\frac{1}{\sqrt{5}}\phi^n-\frac{1}{\sqrt{5}}(-\phi)^{-n}$$

Factoring gives us:

$$F_n=\frac{1}{\sqrt{5}}\left(\phi^n-(-\phi)^{-n} \right)$$

 

[Andrei1]

f_n = 1/sqrt(5)[ϕⁿ - (-ϕ)^-n]

where ϕ = [1+sqrt(5)]/2

Prove that this is the same as $$F_n=\frac{\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n}{\sqrt{5}}$$.

On induction step calculate $$F_{n+1}=F_{n-1}+F_n$$ by using

$$\left(\frac{1+\sqrt{5}}{2}\right)^2=1+\frac{1+ \sqrt{5}}{2}$$

$$\left(\frac{1-\sqrt{5}}{2}\right)^2=1+\frac{1-\sqrt{5}}{2}$$