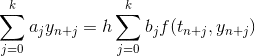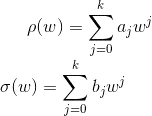SUMMARY
The discussion focuses on the implementation and understanding of generating polynomials in the context of difference equations for ordinary differential equations (ODEs), specifically the three theta methods. Key points include the normalization of coefficients, either by setting a_k = 1 or ensuring sigma(1) = 1. The implicit Euler method is highlighted with the equation sigma(w) = w. Participants emphasize the importance of working through numerous examples to grasp the concept fully.
PREREQUISITES
- Understanding of ordinary differential equations (ODEs)
- Familiarity with difference equations
- Knowledge of numerical methods, particularly the three theta methods
- Basic grasp of generating functions
NEXT STEPS
- Study the derivation of generating polynomials in numerical methods
- Explore the three theta methods in detail
- Learn about the implications of coefficient normalization in ODE solutions
- Review examples of generating functions and their applications
USEFUL FOR
Mathematicians, numerical analysts, and students studying differential equations and numerical methods who seek to deepen their understanding of generating polynomials and their applications in solving ODEs.