Glider pulled by suspended mass

[slapshot151]

Homework Statement

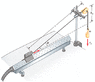
A 1.00-kg glider on a horizontal air track is pulled by a string at an angle θ . The taut
string runs over a pulley and is attached to a hanging object of mass 0.500 kg . (a) Show that the speed v_x of the glider and the speed v_y of the hanging object are related by v_x = uv_y, where u = z(z²–h₀²)^–1/2. (b) The glider is released from rest. Show that at that instant the acceleration a_x of the glider and the acceleration a_y of the hanging object are related by a_x = ua_y.

Homework Equations

v_y²+h₀²=z² (i think...)

The Attempt at a Solution

having problems with part b)
i tried to obtain v_x=uv_y by deriving the following equation by t:

v_y²+h₀²=z²

see attachment for my attempt.

i've been working on this one problem for a few hours now... i don't get it

 

[slapshot151]

anybody?

 

[gneill]

Draw the triangle incorporating z, h_o, and x. What is x in terms of the other variables?

When the hanging mass falls a given distance, what happens to the length of z? How does x change when z changes? How does a change in the length of z relate to the velocity of the falling mass?

Hint: Differentiation is required, and then an application of the chain rule.

 

[SammyS]

anybody?

What you did is called "Bumping" your thread.

Read the https://www.physicsforums.com/showthread.php?t=414380" for PH Forums.

Please don't bump your thread until waiting at least 24 hours.