Hello goochie1234,
The key to working these problems are the following relations:
$$(x,y)=(r\cos(\theta),r\sin(\theta))$$
$$x^2+y^2=r^2$$
The first is obtained directly from the definitions of the sine and cosine functions, while the second is a result of the Pythagorean theorem. Consider the following sketch:
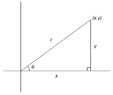
View attachment 954
We have the point $(x,y)$ to which we draw a line segment from the origin, and lalbe its length as $r$. From the point we drop a vertical line segment to the $x$-axis (at the point $(x,0)$ and its length must be $y$.
Using the definition of the sine function on this right triangle, we find:
$$\sin(\theta)=\frac{\text{opposite}}{\text{hypotenuse}}=\frac{y}{r}$$
and so we find:
(1) $$y=r\sin(\theta)$$
Likewise, using the definition of the cosine function on this right triangle, we find:
$$\sin(\theta)=\frac{\text{adjacent}}{\text{hypotenuse}}=\frac{x}{r}$$
and so we find:
(2) $$x=r\cos(\theta)$$
We may also observe that:
$$\frac{y}{x}=\frac{r\sin(\theta)}{r\cos(\theta)}= \tan(\theta)$$
Hence:
(3) $$\theta=\tan^{-1}\left(\frac{y}{x} \right)$$
Note: If $x=0$, then $$\theta=\pm\frac{\pi}{2}$$.
By Pythagoras, we can then easily see:
(4) $$x^2+y^2=r^2$$
So, having these relationships, we can now answer the questions.
1. The rectangular point $(x,y)$ is given. Find the polar coordinates $(r,\theta)$ of this point with $\theta$ expressed in radians. Let $0<r$ and $-2\pi<\theta<2\pi$.
From (3) and (4), we may then state:
$$r=\sqrt{x^2+y^2}$$
$$\theta=\tan^{-1}\left(\frac{y}{x} \right)$$
2.) The letters $x$ and $y$ represent rectangular coordinates. Write the given equations using polar coordinates $(r,\theta)$.
A. $$2r^2\sin(2\theta)=1$$
I would use the double-angle identity for sine $$\sin(2\alpha)=2\sin(\alpha)\cos(\alpha)$$ to rewrite the equation as:
$$4r^2\sin(\theta)\cos(\theta)=1$$
We may rewrite this as:
$$4(r\cos(\theta))(r\sin(\theta))=1$$
Using (1) and (2), we have:
$$4xy=1$$
B. $$2r^2\cos(2\theta)=1$$
I would use the double-angle identity for cosine $$\cos(2\alpha)=\cos^2(\alpha)-\sin^2(\alpha)$$ to rewrite the equation as:
$$2r^2\left(\cos^2(\theta)-\sin^2(\theta) \right)=1$$
Distribute $r^2$:
$$2\left(r^2\cos^2(\theta)-r^2\sin^2(\theta) \right)=1$$
$$2\left((r\cos(\theta))^2-(r\sin(\theta))^2 \right)=1$$
Using (1) and (2), we have:
$$2\left(x^2-y^2 \right)=1$$
C. $$4r^2\sin(2\theta)=1$$
Referring to part A, we see this will be:
$$8xy=1$$
D. $$4r^2\cos(2\theta)=1$$
Referring to part B, we see this will be:
$$4\left(x^2-y^2 \right)=1$$
3.) The letters $x$ and $y$ represent rectangular coordinates. Write the given equation using polar coordinates $(r,\theta)$.
I am going to make assumptions regarding parts A and C based on experience with giving online help and the lack of bracketing symbols that seems to be prevalent.
A. $$r=\frac{5}{\cos(\theta)+\sin(\theta)}$$
Multiplying through by $$\cos(\theta)+\sin(\theta)$$ we obtain:
$$r\cos(\theta)+r\sin(\theta)=5$$
Using (1) and (2), we have:
$$x+y=5$$
B. $$r=5$$
Since $$0<r$$ we may square both sides to get:
$$r^2=5^2$$
Using (4), this becomes:
$$x^2+y^2=5^2$$
Since $r=5$ is the locus of all points whose distance is 5 units from the origin, this result should easily follow.
C. $$r^2=\frac{5}{\cos(\theta)+\sin(\theta)}$$
Multiplying through by $$\cos(\theta)+\sin(\theta)$$ we obtain:
$$r\left(r\cos(\theta)+r\sin(\theta) \right)=5$$
Using (1), (2), and (4) there results:
$$\sqrt{x^2+y^2}(x+y)=5$$
D. $$r^2=5$$
Using (4), this becomes:
$$x^2+y^2=5$$
4.) The letters $r$ and $\theta$ represent polar coordinates. Write the given equation using the rectangular coordinates $(x,y)$.
A. $$r=8$$
Square both sides:
$$r^2=8^2$$
Using (4), we have:
$$x^2+y^2=8^2$$
B. $$0=?$$
I don't know how to interpret this.