Gravitational acceleration in GR

[kvantti]

I tried to search everywhere but couldn't find an answer, so here it goes.

In Newtonian mechanics, the gravitational acceleration g at a distance r from the gravitating object is given by

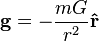
Does this equation apply in general relativity aswel? If not, what is the equivalent in GR, ie. how do you calculate the acceleration due to gravity in GR?

 

[HallsofIvy]

No, not precisely. There is no simple version of that equation in General Relativity. In relativity, there is an equation involving the "Gravitation tensor" which depends upon the metric tensor of the space. From that, you can (theoretically!) find the metric tensor and use that to find the Geodesics in 4-space. All free falling objects move along geodesics with constant "4- speed" which, if you try to force it to a flat 3-space, appears as an acceleration.

 

[DrGreg]

There is an equation in GR

g = - \frac{Gm}{r^2 \sqrt{1 - 2Gm/rc^2}}​

However, the r in that equation is not "radius" in the sense of something you could measure with a stationary ruler next to a black hole. In fact you can't measure such a radius, because any ruler that approached the hole would fall to pieces. r is the circumference of an orbiting circle divided by 2 \pi, which in GR is not the same thing a ruler-measured radius.

Actually proving the formula is no easy thing.



Reference: Woodhouse, N M J (2007), General Relativity, Springer, London, ISBN 978-1-84628-486-1, page 99

 

[A.T.]

There is an equation in GR

g = - \frac{Gm}{r^2 \sqrt{1 - 2Gm/rc^2}}​

However, the r in that equation is not "radius" in the sense of something you could measure with a stationary ruler next to a black hole. In fact you can't measure such a radius, because any ruler that approached the hole would fall to pieces. r is the circumference of an orbiting circle divided by 2 \pi, which in GR is not the same thing a ruler-measured radius.

And would this formula give the acceleration as measured by a local clock, or a distant clock in flat space-time?

 

[George Jones]

And would this formula give the acceleration as measured by a local clock, or a distant clock in flat space-time?

This is the acceleration as measured by the local clocks and rulers of an observer hovering at position r. If such an observer dropped a stone, the observer would measure this (initial) acceleration for the stone.

Note that in the limit Gm/rc^2 is small compared to 1, this acceleration is the same as the Newtonian value.

 

[A.T.]

Thanks!

 

[Passionflower]

There is an equation in GR

g = - \frac{Gm}{r^2 \sqrt{1 - 2Gm/rc^2}}​

However, the r in that equation is not "radius" in the sense of something you could measure with a stationary ruler next to a black hole. In fact you can't measure such a radius, because any ruler that approached the hole would fall to pieces. r is the circumference of an orbiting circle divided by 2 \pi, which in GR is not the same thing a ruler-measured radius.

However the proper distance can be calculated in the Schwarzschild solution for any observer.
The graph below shows the proper distance to the singularity for both a free falling (from infinity) observer and a stationary observer (but note that passed the event horizon there cannot be any stationary observers, but we can still calculate the proper distance passed the event horizon):

[PLAIN]http://img40.imageshack.us/img40/4162/distancestationaryandfr.jpg

 

[pervect]

However the proper distance can be calculated in the Schwarzschild solution for any observer.
The graph below shows the proper distance to the singularity for both a free falling (from infinity) observer and a stationary observer (but note that passed the event horizon there cannot be any stationary observers, but we can still calculate the proper distance passed the event horizon):

[PLAIN]http://img40.imageshack.us/img40/4162/distancestationaryandfr.jpg[/QUOTE]

Note that Pasionflower's notion of "the proper distance" appears to be something that he defined and calculated himself (at least I've never seen him quote a reference deriving it or defining it), and it doesn't appear to agree with, for instance, the Fermi normal distance.

The apparent reason for the disagreement is that the notion of simultaneity for the Fermi normal distance is different than Passionflowers.

On the plus side, the numbers are a lot easier to crunch using Passionflower's definition, it's not a particularly bad approach to measuring distance, it's just not unique. The other big drawback is that it's not computed via a Born-rigid set of observers.

 

[Passionflower]

the Fermi normal distance.

What integral do you use for Fermi normal distance?

My integrals are for 'stationary':
\int _{{\it ri}}^{{\it ro}}\!{\frac {1}{\sqrt { \left| 1-{\frac {{\it <br /> rs}}{r}} \right| }}}{dr}

And free falling (from infinity)
\int _{{\it ri}}^{{\it ro}}\!\sqrt { \left| 1-{\frac {{\it rs}}{r}}<br /> \right| }{\frac {1}{\sqrt { \left| 1-{\frac {{\it rs}}{{\it r}}}<br /> \right| }}}{dr}<br />
which obviously becomes: ro-ri