- #1
independentphysics
- 26
- 2
I am trying to understand gravity inside an exponential axysymmetric mass disk with no thickness.
I know there are exact solutions for this case, such as the Mestel disk or the Kuzmin model, but I want to work out a simpler solution.
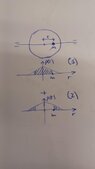
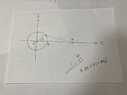
I am approaching the subject by linear superposition. For a mass m inside the disk at a distance r from the center, the gravitational force experienced by the mass m can be divided into the force from the mass M(r) inside the radius r (1), and the force from the mass outside r (2) (see attached image). Due to symmetry, I restrict the solution to a unique axis.
My understanding is that the total gravitational force experienced by the mass m pointing towards the center to the disk, is smaller than the one applying shell theorem (a spherically symmetric body affects external objects gravitationally as though all of its mass were concentrated at a point at its center). Also, it is smaller than the gravitational forced experienced only by the mass inside the radius r (case (1)).
What about gravitational field intensities? My understanding is that the gravitational field intensity at a distance r is bigger than just for case (1). Is it also bigger than for the case of all the mass of the disk concentrated at a point?
I know there are exact solutions for this case, such as the Mestel disk or the Kuzmin model, but I want to work out a simpler solution.
I am approaching the subject by linear superposition. For a mass m inside the disk at a distance r from the center, the gravitational force experienced by the mass m can be divided into the force from the mass M(r) inside the radius r (1), and the force from the mass outside r (2) (see attached image). Due to symmetry, I restrict the solution to a unique axis.
My understanding is that the total gravitational force experienced by the mass m pointing towards the center to the disk, is smaller than the one applying shell theorem (a spherically symmetric body affects external objects gravitationally as though all of its mass were concentrated at a point at its center). Also, it is smaller than the gravitational forced experienced only by the mass inside the radius r (case (1)).
What about gravitational field intensities? My understanding is that the gravitational field intensity at a distance r is bigger than just for case (1). Is it also bigger than for the case of all the mass of the disk concentrated at a point?