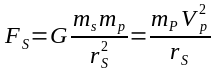I need some support, please, for a gravity assist analysis

[LesRhorer]

TL;DR Summary

A gravity assist is not a two body problem. It is a three body problem, but this i not clear to many people.

I am having a discussion with a couple of very obtuse individuals on another forum who think they know celestial mechanics, but do not. These two have long promoted themselves to be something they are not, and since I am rather new on the forum they are unwilling to even listen (or heaven forbid admit they are wrong), and much of the rest of the forum believes their story, since none of the rest are physicists. It would be absolutely wonderful if someone here with official credentials could back me up in the discussion. The most wonderful support would be if someone could devote just a few minutes to join in a voice chat or provide a very short video covering the situation. Barring that, a brief message clearly explaining the situation would suffice. Great thanks in advance for any help. Note I do know a moderate bit of Physics. I studied Mathematical and Applied Physics for four years starting in 1977 before deciding to quit and enter industry.

For simplicity we will, assume purely gravitational interactions. No rocket engines will be fired. All the objects are simple spheres of uniform density with no significant atmospheres.

The two body problem:
We have two objects P(rimary) and V(ehicle). Object P has a very large mass and V a comparatively small mass so the force applied by V to P throughout its trajectory is insignificant. P is not accelerating (it is in free space). We know the force between the objects at any point throughout V's trajectory is:

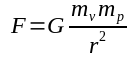
We also know the energy added to or taken away from V as it heads toward and away from P, respectively, is given by:

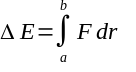
(F and R are both vectors, of course, and the integrand is a scalar product, but I don't know how to show vectors or dot products here.) If we take k to be the distance for perigee of V from P, and we take l to be some arbitrary distance from P along V's path, then the kinetic energy gain by V on its inbound path is

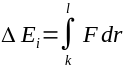
it's outbound loss in energy is

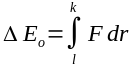
but that is equal to

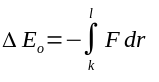
The total energy change, then, from any point along V's inbound path to a point along the outbound path with the same displacement is

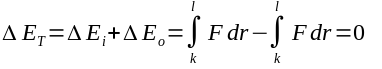
Since in any neutral two body system there is no other force than this one gravitational attraction, this is the only source of energy or momentum in the system. Unlike the two correspondents believe, changing the frame of reference has no mechanical effect. It is of course true one can easily change the initial and final values of the velocity vectors for V, the CHANGE in energy, speed, and magnitude of the momentum is zero for all inertial reference frames. One gains nothing other than a change in direction, so there is no point in swinging around a free body in space in an attempt to increase velocity. In addition, although P can have any arbitrary velocity we like relative to some external frame of reference,it has zero orbital angular momentum, so the vector product of V's orbital angular momentum with P's is zero, meaning the entire path of V's orbit is contained within a single orbital plain. This is true whether V's orbit is elliptical (below P's escape velocity) or hyperbolic (above P's escape velocity).

The three body problem:
If we add in a third, extremely large body S, then of course we have a three body problem. Now, classical three body problems can be devilishly difficult to solve, but we have already taken V to be small enough to have negligible effect on P, let alone S, and S is also taken to be large enough that P has no significant effect on it. We just now calculated the behavior of the V/P system about it's barycenter (effectively the center of mass of P), but now we see the entire V/P system is also orbiting S. This motion is not a linear motion and so is not frame dependent. It is unique. In particular, for a circular orbit:

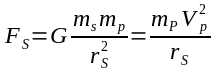
Rearranging, we get:

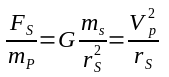
This is the gravitational field strength due to S at the V/P system's orbit. Note this value is the same for every object at this distance from S. It is completely independent of the mass of any object other than S. Solving for the orbital velocity we get:

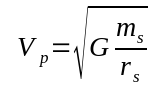
In the case of our Sun, at Mars' orbit, the value is about 24,130 meters/sec, or about 54,000 mph. For a rule of thumb, this is the amount of speed boost one may obtain in a slingshot maneuver with Mars. For Jupiter, it s about 29,000 mph The Voyager spacecraft had initial velocities of around 35,000 mph, but after encounters with a couple of planets (PLANETS, not free bodies) their velocities were able to exceed solar escape velocity, which would be the equivalent of travelling more than 94,000 mph leaving Earth orbit, or an effective increase of considerably more than 60,000 mph by flying near the outer planets. If it had flown near a huge body out in free space, it would have experienced zero increase in speed.

Furthermore, the planets and any small body near them, because they are in orbit around the Sun, have angular momentum, and the vector product of the angular moment of the system's orbit and V's angular moment can result not only is a large increase or decrease in speed WRT the Sun, it can produce a resultant acceleration with a component perpendicular to V's original orbit, meaning the vehicle can exit the plane of the ecliptic. This precisely what Voyager I did, and it is now on a trajectory inclined some 35 degrees to the plane of the ecliptic.

There are a virtual plethora of discussions on this topic around the web (and even on this forum), but all of them pretty much gloss over the fact there absolutely must be a third very large body involved. They all pretty much talk about planets or moons, but none explicitly point out it can ONLY be done with a planetary body. So is there anyone here that would care to join me for a few minutes to back me up in a discussion on this topic? Barring that, can someone here provide at least a message affirming the things I have demonstrated here? A direct quote from a textbook on celestial mechanics would work very well, also

 

[jbriggs444]

We do not do third party rebuttals here.

I can imagine correct arguments by your opponents. I can imagine incorrect arguments by your opponents. Since they are not here to defend themselves, we ought not engage.

 

[Baluncore]

Texts on celestial mechanics discuss gravity assist as a three body problem. That must be the case. Even wikipedia refers to gravity assist as a three body problem.
https://en.wikipedia.org/wiki/Gravity_assist#Tisserand_parameter_and_gravity_assists

There will always be deluded people who cannot be helped. Don't waste your time and energy. Ask them to explain gravity assist, without referring to the third body or a fixed reference frame.

 

[A.T.]

A gravity assist is not a two body problem. It is a three body problem, but this i not clear to many people.

Is this just a categorization issue that you are having? Seems like your definition of two/three body assumes that one of the bodies has negligible mass, which is not the general case. It's a matter of convention if you count that test mass or not in your naming scheme, but who cares what it is called, as long you do the math right.

 

[Vanadium 50]

Seems like your definition of two/three body

Well, the point is moot for large values of two and small values of 3.

A gravity assist is an elastic interaction between bodies 1 and 2 so that kinetic energy in the system between bodies 2 and 3 is transferred to 1. You can consider it a three body interaction or a pair of two body interactions. Up to you.

However, I think we should not debate by proxy. That has three sides and not just two.

 

[Dale]

I thought that it was considered a one body problem. I thought the categorization was determined by the number of bodies with a significant gravitational potential. There is one gravitating mass, one negligible mass, and a reference frame.

I agree that the categorization doesn’t matter, just the math.

 

[LesRhorer]

We do not do third party rebuttals here.

I can imagine correct arguments by your opponents. I can imagine incorrect arguments by your opponents. Since they are not here to defend themselves, we ought not engage.

Nowhere did I request any rebuttal, at all, and certainly not in this forum, unless of course I have made some mistake and someone here would be so kind as to point it out. I asked for support, not a rebuttal. I am fighting a battle completely by myself, there being no one on the on the other forum who really understands Physics at this level, or even at an entry undergraduate level. The really frustrating thing is most of the participants do not even understand high school level Physics, and that definitely includes these two folks, despite the fact the one who calls himself Rocket Scientist claims to be responsible for launching satellites (cubesats) as his profession. I am skeptical, although actually it is possible he does. He seems to understand math pretty well.

His mathematical arguments are correct. It is their application that is all wrong. He thinks all he has to do is ascribe some velocity to the Primary and then apply the formula., which is in and of itself quite simple, actually. He thinks that by simply choosing a different reference fame he can demonstrate an effective acceleration of V. It s true, of course, that one can easily choose a different reference frame where, say, the initial velocity of V is zero, in which case the final velocity of V in that frame is twice the initial velocity of V relative to P. It is a simple Galilean transform, and results in no change in acceleration. He refuses to understand or acknowledge the effect of an orbital system and the difference it makes. He repeats endlessly, "It doesn't matter how the Primary gets its velocity", insisting there is no difference in this respect between an object with a linear velocity of 10 Km/s and one with a tangential orbital velocity of 10 Km/s.

The bottom line here, however, is I am not asking for someone to bash this guy in this forum. That would indeed be completely improper. I am asking for just a little support - preferably credentialed support - in the other forum. I cannot, I WILL not claim credentials I do not have. The rebuttal I face in the forum is then,
'He does this for a living! Why should we believe you?" Consequent to that attitude comes a lot of ridicule, which doesn't really concern me, but also a widespread belief in fractured science - almost pseudoscience - which absolutely does concern me.

 

[LesRhorer]

I thought that it was considered a one body problem. I thought the categorization was determined by the number of bodies with a significant gravitational potential. There is one gravitating mass, one negligible mass, and a reference frame.

I agree that the categorization doesn’t matter, just the math.

No, it absolutely requires three gravitationally active bodies. Because the effect on the giant body is negligible, we can simply state the barycenter of the two smaller bodies has an orbital velocity, and indeed that is how the respondent in the other forum is proceeding. The very fact the two bodyt system must be externally accelerated makes it (at a minimum) a three body problem is glossed over by him insisting any velocity - including a liner one - can be used in the formula. This should be inferred by anyone studying a gravity assist problem. The fact he does not is an error in physics, (quite an obvious and fundamental one) not mathematics. His math - or I should say the math I expect someone has given to him - is fine. His physics is total nonsense.

 

[Dale]

It seems like you are making it way more difficult than it needs to be. You can simply treat it as an elastic collision.

 

[LesRhorer]

Well, the point is moot for large values of two and small values of 3.

A gravity assist is an elastic interaction between bodies 1 and 2 so that kinetic energy in the system between bodies 2 and 3 is transferred to 1. You can consider it a three body interaction or a pair of two body interactions. Up to you.

However, I think we should not debate by proxy. That has three sides and not just two.

Both points are absolutely correct. That is why I am asking for a few minutes of someone's time to address the issue in the other forum. The preferred assistance would be a live voice or video chat with me and the other participants in the other forum. One or two formal messages detailing how and why this is indeed a three body problem from a professional physicist or astronomical engineer would be good, as well. The only issue is the folks there tend not to read anything with more than a few sentences, but I will take what I can get.

 

[LesRhorer]

It seems like you are making it way more difficult than it needs to be. You can simply treat it as an elastic collision.

Incorrect. That is PRECISELY what he is doing. He even says so, verbatim. An elastic collision results in no change in energy or momentum. One of the two major advantages of a gravity assist is it is NOT elastic. Not at all. Object V undergoes a massive change in momentum, and energy. Of course, overall, both momentum and energy are conserved. The change in momentum is reflected by a precisely opposite change in momentum of the Primary, but compared to the total momentum of the Primary, the change is totally insignificant. If this is treated as an elastic collision then we do indeed have merely a two body problem, but in that case, V would merely be in orbit around P - a hyperbolic one, rather than elliptical if V's velocity is high enough. This is not what happens. Instead, V flies off either at a much greater speed than it had coming toward P, or at an angle to the plane of its original orbit around P, or both.

 

[LesRhorer]

Is this just a categorization issue that you are having? Seems like your definition of two/three body assumes that one of the bodies has negligible mass, which is not the general case. It's a matter of convention if you count that test mass or not in your naming scheme, but who cares what it is called, as long you do the math right.

Doing the math correctly requires applying the physics correctly. Despite his continually incorrect arguments, this will not work for a vehicle passing a large body in deep space. In that example, no gravity assist occurs. The vehicle leaves the vicinity of the massive body with precisely the same energy and magnitude of momentum as it approached. Only if the entire system consisting of both bodies is being accelerated by an external gravitational field will the vehicle gain (or lose) additional energy.

Generally, the calculation is only performed on the V/P system by presupposing a specific orbital velocity, but irretrievably embedded in the very fact is an extremely large third (or more) body. Just because one does not offer any details of the third body does not mean it is not required for it to exist. Indeed, this is the issue with the vast majority of online treatments of the issue. They do always talk about planets or in some cases a large moon or asteroid. They never do talk about a star or a large body in free space. The implicit assumption is the very large body does exist, but because it is not explicit, lots of people miss the very fact the effect is not one available in deep space, or around a star. Slingshoting around the Sun is not a gravity assist. It is just an orbit. It can most certainly be used to change the direction of the momentum vector, but never the magnitude.

And yes, of course this is not the general case. That is why the approximation to the Jacobi constant for a restricted three body problem can be invoked. As we all should know, there is no general solution to an N-body problem where N > 2. If, however, we restrict the parameters for the bodies in question, we can produce a close approximation using much simpler forms. A solar system with a huge star at the center and comparatively small, widely spaced planets orbiting the star is an example. So is a gravity assist for an intra-planetary vehicle.

 

[LesRhorer]

Texts on celestial mechanics discuss gravity assist as a three body problem. That must be the case. Even wikipedia refers to gravity assist as a three body problem.
https://en.wikipedia.org/wiki/Gravity_assist#Tisserand_parameter_and_gravity_assists

There will always be deluded people who cannot be helped. Don't waste your time and energy. Ask them to explain gravity assist, without referring to the third body or a fixed reference frame.

Yes, I used that very link in my discussion. He of course hand waves it, claiming he knows it thoroughly while not understanding it at all. If it were just him and his toady, I suppose I could grudgingly ignore it. It is not just him, however. He has essentially the entire forum believing he is an authority on Astrophysics and taking his word for it because of the fact. What is even worse is the entire forum is one more or less directed at debunking such derp as flat Earth, anti-vax, etc, His behavior in the forum is nearly identical to a true believer, offering blank statements with no support, insulting almost everyone, and getting extremely angry whenever he is contradicted. If we cannot help him to actually understand some physics, then it is a bit of a sad thing, but such is life. Exposing him as a charlatan and a poser is another matter entirely. The forum is made up primarily of rational people who reject pseudo-science. They are being duped by this guy to think he is literally a rocket scientist. He may actually be a participant in a team that hands over cubesat packages for launch into LEO by one of the space agencies. I don't know. That, however, requires virtually zero understanding of celestial mechanics. The space agency does all the work. All one needs is a small package and about $30,000 per kilogram. In my estimation, he is definitely a blowhard, and I am skeptical of the majority of his claims -which are almost always steeped in hyperbole. I know for a fact none of his expositions conform to an understanding of even high school physics, let alone celestial mechanics.

 

[Dale]

An elastic collision results in no change in energy or momentum.

It certainly does. Both energy and momentum are transferred between objects in an elastic collision.

One of the two major advantages of a gravity assist is it is NOT elastic. Not at all.

This is wrong. There is no energy dissipation, so it is indeed elastic.

Of course, overall, both momentum and energy are conserved.

This is why it is elastic.

It seems like you have some misconceptions about elastic collisions. It is perfectly acceptable to describe a gravitational assist as an elastic collision.

V would merely be in orbit around P - a hyperbolic one, rather than elliptical if V's velocity is high enough. This is not what happens. Instead, V flies off either at a much greater speed than it had coming toward P

This is simply a hyperbolic orbit in a different frame.

 

[LesRhorer]

It certainly does. Both energy and momentum are transferred between objects in an elastic collision.

First of all, I hesitate to speak of it as a collision. In ordinary usage, a collision tends to connote a very brief, perhaps virtually instantaneous interaction, not something that spans weeks, months, or even years. It almost always implies an impact, but of course does not necessarily have to be defined as such.. Speaking most broadly, the entire 14 billion long history of the universe is a collision, but it doesn't lend much understanding to characterize it as such. Leaving semantics aside, however, the fact is in the frame of reference of the barycenter of the two smaller bodies, the interaction is not elastic. Object V either picks up or drops a rather large amount of energy. This can only be true if the barycenter of the two smaller objects is not in an inertial frame of reference, but rather is being acted upon by an external force in addition to the gravitational force between the smaller objects.

Obviously, in a mechanical collision there is not usually any transverse displacement (displacement perpendicular to the initial velocity vector) and there is never any force exerted on the components after the event is completed. Consequently, there is also no acceleration of any component once the event is complete. Except at the moment of impact, all of the trajectories are linear. None of this is true in a 2 body gravitational system, which is IMO another good reason not to classify it as a collision. It s an interaction that properly speaking continues for all time.

Oh, and your statement above is not very informative. While it is true energy and momentum are transferred between objects in an elastic collision, it is also true in an inelastic collision and in fact is generally true in almost any dynamic system. A two body system is indeed elastic unless the orbit of one body intersects the other body, in which case it definitely is a collision, and very likely not elastic. All of that is beside the point, however

This is wrong. There is no energy dissipation, so it is indeed elastic.

Fundamentally speaking, there is no such thing as an inelastic interaction in classical mechanics. For convenience and simplicity of analysis, we can separate potential energy from the initial kinetic energy and say an interaction is inelastic if one or more bodies give up kinetic energy to be translated into potential energy, or we can also talk about transferring kinetic energy away from the original components to one or more additional components. This is the case, for example, if one or both of the two original components shatters or permanently deforms due to having exceeded the elastic limit of the material of which it is made, or if some component is semi-fluidic and kinetic energy is translated onto a vast number of smaller particles. We call that heat. All the energy is still there, it just is no longer associated only with the kinetic energy of the N initial components. Similarly, if one or all of the original components is under compression (potential energy) and the collision causes the compression to be released at impact, the original two components can fly apart at a greater velocity than their original closure rate. Again, this is inelastic in the sense the final kinetic energy of the system is not the same as the initial kinetic energy. Inelastic interactions do not have to be dissipative with respect to the kinetic energy of the colliding objects.

If we only consider the two smaller bodies in our ultimate analysis, i.e. a two body problem, then the interaction is not elastic. The maneuver results in quite a significant increase or decrease) in kinetic energy and momentum for the entire V/P system in its own frame of reference, although of course the change for the small body is much greater in comparison to its initial momentum. If object P is very large compared to V, then while the change to the momentum of P relative to S is virtually equal to the change in momentum of V compared to S, this change in momentum is so tiny compared to the total momentum of P as to be totally insignificant.

This is why it is elastic.

First of all, it is only elastic if we include the potential energy as well as kinetic energy. In total, each Voyager spacecraft gained considerably more than 27 Km/s throughout their journey, or more than 513 Gigajoules of energy "stolen" from the orbital momentum of Jupiter and Saturn. Since their encounters with those planets, almost all of that has been translated back into potential energy, so that neither spacecraft is travelling all that much faster than at the end of the rocket burn which sent them towards Jupiter.

Allowing for this by taking both kinetic and potential energy into account, their trajectories are absolutely elastic in terms of the total energy of the Sun, both planets, and the spacecraft themselves. They are also elastic in terms of the total momentum and energy exchanged at each flyby with each planet. They are absolutely not elastic in terms of the energy available to an orbiting body in a two body system, which is zero. The craft extracted far, far more energy from their interactions with the planets than would have been available had the planets not been in orbit around the Sun. In particular, more than 513 Gigajoules of kinetic energy versus zero.

It seems like you have some misconceptions about elastic collisions. It is perfectly acceptable to describe a gravitational assist as an elastic collision.

Only as long as every significant force exerted to the objects are taken unto account. The gravitational forces exerted by all three bodies must be part of the calculations. Since the Sun is extremely large compared to Jupiter, Saturn, and the Voyager spacecraft, those forces on the Sun can be ignored. The forces exerted on Jupiter and Saturn by Voyager I and II can also be ignored. The rest cannot. In fact, the ONLY long range effect on the speed of Voyager I and II are a direct result of the Sun's gravitational force. The gravitational influence of the planets affect only the direction of Voyager's momentum at any given distance from them.

This is simply a hyperbolic orbit in a different frame.

Not unless the frame in question is highly non-inertial. It certainly is not a classical Euclidean conic section, by any means. It is more like a wire frame hyperbola (or ellipse, if V is going somewhat slower). that has been stomped on by someone. First of all, Voyager I was inflected 35 degrees out of the plane of the ecliptic when it reached Saturn. Ignoring the portion f the journey when Saturn's gravitational attraction exceeded the Sun's attraction on Voyager I, the path looks like an intersection of two partial hyperbolas sitting at a 35 degree angle to each other. Add in the section where Saturn dominated, and there is a union of two hyperbolas that make a sort of flattened out hyperbola near the planet. Voyager II was not directed out of the plane of the ecliptic, but its path still is the union of four different hyperbolas, each with very different curvatures at their vertices determined by the vector sum of the forces exerted by the planet and the Sun.

When only two bodies are significantly involved, we get a nice, simple, conic section; either an ellipse or half of a hyperbola. Whenever there is more than 1 point source of gravity acting upon an object, the path can be twisted into all sorts of shapes. The simplest example is if the gravitational source is an infinite plane. Then the trajectory is a parabola. Hmm. Now where have I seen that before? Sarcasm aside, the point is any N-body system will display orbits that approximate ellipses and / or hyperbolas WRT the barycenter of the system for some fractions of each orbit, but the orbits are not typically at all well modeled by either ellipses or hyperbolas for the entire trajectory of each body. Only those sections of each orbit where a single body dominates can be approximated by a simple conic section. I think we all realize no real-world form can be perfectly modeled by a classical geometric form, but calling the trajectory of an object that is part of an N-body system a "hyperbola" is really stretching it, no pun intended.

No matter how one slices, dices, smashes, or purees it, a gravitational assist (as opposed to a simple orbit) requires at a minimum three bodies.

 

[Drakkith]

No, it absolutely requires three gravitationally active bodies. Because the effect on the giant body is negligible, we can simply state the barycenter of the two smaller bodies has an orbital velocity, and indeed that is how the respondent in the other forum is proceeding. The very fact the two bodyt system must be externally accelerated makes it (at a minimum) a three body problem is glossed over by him insisting any velocity - including a liner one - can be used in the formula. This should be inferred by anyone studying a gravity assist problem. The fact he does not is an error in physics, (quite an obvious and fundamental one) not mathematics.

Forgive me, but why can't two objects in free space take part in a gravitational assist? If a very large body is moving to the left (-x direction), a very small body is moving up (+y) direction, and they pass very close to one another such that the path of the small body is changed by, say, 60 degrees in the direction the large body is moving, is that not a gravitational assist?

 

[Drakkith]

Playing around in an empty setting in Universe Sandbox, I can impart nearly 6 km/s to an asteroid by having the Earth pass close by it at 10 km/s. That is, initially the asteroid's speed is 0 m/s relative to the origin and Earth is moving at 10 km/s relative to the origin, velocity vector <0, 0, -10> km/s. Simulation starts with the asteroid at 0.01 AU from Earth. The Earth passes very close to the asteroid, accelerating it. By the time the asteroid is 0.01 AU from Earth again it has a velocity of 5.93 km/s and a velocity vector of <5.66, 0, -1.76> km/s relative to the origin. Relative to the Earth, the asteroid starts and ends with a velocity of 10 km/s, with a final velocity vector of <5.66, 0, 8.24> km/s.

Is this not a 2-body gravitational assist?

 

[LesRhorer]

No, it s not, by definition of what we mean by a gravity assist. Certainly, a single large body can be employed to do nothing more than change the direction of a spacecraft. This is not what is meant by a gravity assist, and it would be at best marginally useful in intra-planetary travel. If one wishes to go a different direction, just wait for a different time to launch. Fortunately, as long as the planet is in fact in orbit, one gains not only a change in direction, but typically a doubling in speed, as well.

A gravity assist is a maneuver that changes the speed of a spacecraft by a significant amount without having to use any fuel. In order to leave Earth and sail out of the solar system from Earth, Voyager I and II would have had to have initial velocities substantially in excess of 90 Km/s (200,000 mph). While not exactly impossible, the size of the rocket booster would have had to be far more than 50 times bigger than the ones used. The upside would have been it would have taken far less time to leave the solar system, but we wanted to have layovers, as it were, at Jupiter and Saturn in the first place. This being the case, we were able to assemble a rocket booster at a small fraction of the cost and merely get the spacecraft up to about 13 Km/s (30,000 mph) when it reached Jupiter's vicinity. In fact, it was even easier still because we did not have to fight the Sun's gravity all the way. The path to Jupiter was one which was in part sunward. Rather than taking a path directly along the line between the Sun and Earth, the path was much closer to being along Earth's orbit, meaning the craft started out with a velocity of 29.7 Km/s (107,000 mph) at the outset, and only needed enough of a boost so they were still going around 13 Km/s by the time they reached Jupiter. The encounter with Jupiter boosted the velocity by something like 10 Km/s, roughly doubling their speed at that point. A similar thing happened at Saturn, although since Saturn's orbital velocity is much smaller than Jupiter's, the change in velocity was much less.

Notice it can also be used as a braking maneuver. The satellites we send sunward are usually going much to fast by the time they reach their destination. The gravity of Earth, Venus, and Mercury are usually used to slow down those spacecraft.

A homework problem for the student: How much energy will a 0.8 ton spacecraft lose when traveling from Earth to Jupiter?

 

[wrobel]

There are a lot of systems where both momentum and energy conserved but it would be strange to call them all elastic collisions.

 

[weirdoguy]

by definition of what we mean by a gravity assist.

Which, as we can see, can change depending on who you ask. Definitions are not something given from "abave", these are man-made constructs.

 

[PeroK]

No, it s not, by definition of what we mean by a gravity assist. Certainly, a single large body can be employed to do nothing more than change the direction of a spacecraft.

That is essentially what a gravity assist does (in the reference frame of the planet).

This is not what is meant by a gravity assist, and it would be at best marginally useful in intra-planetary travel. If one wishes to go a different direction, just wait for a different time to launch. Fortunately, as long as the planet is in fact in orbit, one gains not only a change in direction, but typically a doubling in speed, as well.

Speed is frame dependent. The interaction between the spacecraft and the planet is a two-body problem in which only the direction of the spacecraft changes.

However, when the interaction is analysed in a frame where the planet is moving, the speed of the spacecraft may increase or decrease.

 

[Drakkith]

No, it s not, by definition of what we mean by a gravity assist. Certainly, a single large body can be employed to do nothing more than change the direction of a spacecraft.

But my simulation in Universe Sandbox changed both the speed and direction... the asteroid gained nearly 6 km/s in speed.

 

[PeroK]

But my simulation in Universe Sandbox changed both the speed and direction... the asteroid gained nearly 6 km/s in speed.

That's in a frame where the planet is moving. Which is the whole point. In the Earth frame the asteroid will only change direction.

 

[LesRhorer]

Playing around in an empty setting in Universe Sandbox, I can impart nearly 6 km/s to an asteroid by having the Earth pass close by it at 10 km/s. That is, initially the asteroid's speed is 0 m/s relative to the origin and Earth is moving at 10 km/s relative to the origin, velocity vector <0, 0, -10> km/s. Simulation starts with the asteroid at 0.01 AU from Earth. The Earth passes very close to the asteroid, accelerating it. By the time the asteroid is 0.01 AU from Earth again it has a velocity of 5.93 km/s and a velocity vector of <5.66, 0, -1.76> km/s relative to the origin. Relative to the Earth, the asteroid starts and ends with a velocity of 10 km/s, with a final velocity vector of <5.66, 0, 8.24> km/s.

Is this not a 2-body gravitational assist?

Not a correct one, no. There is no such thing as an asteroid travelling at 0 Km/s. Any asteroid is going to have an orbital velocity of about 20+ Km/s. Something has to get rid of a very substantial amount of that energy and much of its potential energy without tearing the asteroid apart. That is quite unrealistic at the outset, but we will set that aside. By the time it reaches Earth's orbit, some 78 million Km or so closer to the Sun at an average of about 0.015 m/sec^2 , it will be moving at quite a clip, depending on just what sort of orbit the asteroid manages to attain. That also said, the most important parameter is not the object's velocity WRT the Earth. No matter what that velocity is (as long as it is high enough not to hit the Earth), the change in speed due to Earth's gravity will be the same when the object leaves Earth as it was when the asteroid approached the Earth.

So far, so good.

The failure is, the Earth is not stationary. It is accelerating due to the Sun's gravity, and so is the asteroid at nearly exactly the same rate. I don't see where the parameters above specify the angle between the asteroid's trajectory WRT the Earth and the Earth's orbital path. It makes a huge difference all the way around. The Earth's orbital velocity is 29.78 Km/s, which taking an Earth-relative velocity of 10 m/s means the asteroid's initial velocity WRT the Sun can be anything from 19.78 Km/s to 39.78 Km/s. After the encounter, the speed of the asteroid can be anything from -19.78 Km/s (back towards from where it came) up to 39.78 Km/s, depending upon the angle between the initial trajectory and the Earth's' trajectory. If the magnitude of the final calculated velocity is below around 11.2 Km/sec, it will hit the Earth sooner or later. What's more, if the initial trajectory of the asteroid is not directly parallel or antiparallel to the Earth's orbit, then the asteroid will deflect away from the plane of the ecliptic out towards the intra-galactic void. Of course, if its velocity is much under 30 Km/s, it won't be heading that way for long.

So no, the path of a rogue asteroid around a planet cannot be calculated using only the object's initial velocity and the planet's gravitational field strength. Indeed, other than the fact the planet's mass must be much, much greater than the asteroid's mass and the asteroid must be going fast enough to overcome the planet's gravity, the planet's gravity is essentially irrelevant to the change in the asteroid's speed. It does make a difference to the shape of the asteroid's trajectory.

 

[Drakkith]

Not a correct one, no. There is no such thing as an asteroid travelling at 0 Km/s.

That's easily fixable by simply changing to a reference frame where both the Earth and the asteroid are moving. If our reference frame is moving at -5 km/s in the Z direction relative to the origin in Universe Sandbox, then the Earth is moving at -5 km/s relative to our frame and the asteroid is initially moving at +5 km/s relative to our frame. The choice of 0 km/s for the asteroid was simply convenience for getting the close flyby correct.

No matter what that velocity is (as long as it is high enough not to hit the Earth), the change in speed due to Earth's gravity will be the same when the object leaves Earth as it was when the asteroid approached the Earth.

...relative to the Earth. Not relative to the frame of the coordinate system I was using. This is true of all gravity assists.

The failure is, the Earth is not stationary. It is accelerating due to the Sun's gravity, and so is the asteroid at nearly exactly the same rate.

Which would seem to suggest that my simulation where the Earth and the asteroid were the only objects is a very good approximation of reality. You can't seriously suggest that the results would be wildly different if we were to place a star 1 AU away?

I don't see where the parameters above specify the angle between the asteroid's trajectory WRT the Earth and the Earth's orbital path. It makes a huge difference all the way around. The Earth's orbital velocity is 29.78 Km/s, which taking an Earth-relative velocity of 10 m/s means the asteroid's initial velocity WRT the Sun can be anything from 19.78 Km/s to 39.78 Km/s.

The asteroid approached the Earth very close to 'head on'. It was offset just enough from in front of the Earth's path that it didn't impact the Earth at perigee.

If the magnitude of the final calculated velocity is below around 11.2 Km/sec, it will hit the Earth sooner or later.

No, that's the escape velocity of Earth at the surface. At 0.01 AU it is much less than the 10 km/s it was traveling relative to Earth. The asteroid was on a hyperbolic orbit and stayed that way.

What's more, if the initial trajectory of the asteroid is not directly parallel or antiparallel to the Earth's orbit, then the asteroid will deflect away from the plane of the ecliptic out towards the intra-galactic void.

None of this addresses the fact that the asteroid had 0 kinetic energy relative to coordinate system frame before the flyby and much more than zero after. Again, how is this not a gravity assist?

 

[A.T.]

The failure is, the Earth is not stationary. It is accelerating due to the Sun's gravity, and so is the asteroid at nearly exactly the same rate.

And because they both accelerate due to the Sun's gravity at nearly exactly the same rate, you can analyze their interaction locally in a free falling frame fixed to their common center of mass. It's an approximation, but so is ignoring the fact that our entire solar system orbits the center of the galaxy.

 

[LesRhorer]

That's in a frame where the planet is moving. Which is the whole point. In the Earth frame the asteroid will only change direction.

Close, but not quite. If the Earth's frame of reference were inertial, it would be the case, but it is not. Even in the Earth's frame of reference, the speed of the asteroid can increase or decrease a huge amount. Over small distances, like shooting a gun or throwing a ball, we can easily ignore the Sun's relatively small acceleration of 0.0177 N/Kg. (It is significant for ocean tides, however). In celestial mechanics, however, this amount of force per unit Kg cannot be ignored, especially when the total gravitational influence of a planet over a large distance adds up to zero.

To look at it another way, the gravitational field of any single isotropic spherical object is symmetrical. This means the trajectory of any object influenced only by the gravity of the first object is also going to be perfectly symmetrical in both shape and velocity. If we add any object of significant size nearby, it is going to perturb the trajectory of both the first and second objects. How much depends on how big and how close. If any two objects in a system are of sufficiently large mass and relatively small distance compared to that size, the trajectories are no longer going to be symmetrical. That is why the N-body problem is so damned hard in general. In these cases, however, we can ignore the effect of all the planets on the Sun, since it is so huge, and similarly ignore the effect on each planet on every other since they are relatively much smaller and so far from each other, and totally ignore the effect of a tiny spacecraft on everything. For intra-planetary travel, we can never ignore the Sun and wind up with anything like an accurate prediction. Thus: three bodies.

 

[PeroK]

Close, but not quite. If the Earth's frame of reference were inertial, it would be the case, but it is not. Even in the Earth's frame of reference, the speed of the asteroid can increase or decrease a huge amount. Over small distances, like shooting a gun or throwing a ball, we can easily ignore the Sun's relatively small acceleration of 0.0177 N/Kg. (It is significant for ocean tides, however). In celestial mechanics, however, this amount of force per unit Kg cannot be ignored, especially when the total gravitational influence of a planet over a large distance adds up to zero.

To look at it another way, the gravitational field of any single isotropic spherical object is symmetrical. This means the trajectory of any object influenced only by the gravity of the first object is also going to be perfectly symmetrical in both shape and velocity. If we add any object of significant size nearby, it is going to perturb the trajectory of both the first and second objects. How much depends on how big and how close. If any two objects in a system are of sufficiently large mass and relatively small distance compared to that size, the trajectories are no longer going to be symmetrical. That is why the N-body problem is so damned hard in general. In these cases, however, we can ignore the effect of all the planets on the Sun, since it is so huge, and similarly ignore the effect on each planet on every other since they are relatively much smaller and so far from each other, and totally ignore the effect of a tiny spacecraft on everything. For intra-planetary travel, we can never ignore the Sun and wind up with anything like an accurate prediction. Thus: three bodies.

You came here for approbation and all you've found are the same counter arguments to your misconceptions that you must have got on the other forum.

Perhaps that tells you something.

 

[A.T.]

For intra-planetary travel, we can never ignore the Sun and wind up with anything like an accurate prediction. Thus: three bodies.

You don't ignore the Sun for the whole travel, just for the local interaction. If that is not accurate enough, then you might just as well include all the planets, because three bodies require numerical methods anyway.

 

[weirdoguy]

Perhaps that tells you something.

That physicists don't know what they're talking about

 

[PeroK]

If the Earth's frame of reference were inertial, it would be the case, but it is not.

The Earth is in a free fall orbit of the Sun. You don't get much more inertial than that.

Honestly, you're missing the basics of vector kinematics and analysis in more than one (inertial) reference frame.

 

[LesRhorer]

And because they both accelerate due to the Sun's gravity at nearly exactly the same rate, you can analyze their interaction locally in a free falling frame fixed to their common center of mass. It's an approximation, but so is ignoring the fact that our entire solar system orbits the center of the galaxy.

Nope, not even a little. Not even close. The orbital motion of the barycenter of the planet / asteroid system is crucial, especially since the net effect of the planet's gravity on the asteroid's speed is dead zero. Once again, the planet's effect on the speed of the asteroid at any given displacement from the planet is absolutely zero. A free body cannot under any circumstances change the orbital energy of any object under its influence. If we have a large object in free space and a smaller object is heading toward it, the inbound speed of the smaller object at 100,000 kilometers will be perfectly equal to the outbound speed at 100,000 kilometers. For a given pair of masses, the energy of the system is ONLY dependent upon their separation. Add in a third extremely massive object, and suddenly the energy of the first object has effectively nothing to do with the second object, as opposed to it being only due to the second object before the appearance of the third object. It is the same with the momentum. The momentum of the barycenter of the two body system in the frame of reference of the first body is essentia;ly only due to the movement of the second body relative to the barycenter. Plop in a giant third object, and the barycenter is suddenly nowhere near either of the first two bodies. The momentum of the first object relative to the barycenter suddenly jumps from an infinitesimal value to some truly giant value depending on the actual mass of the first and third objects and their separation. The net acceleration of the second body jumps from zero to three times the orbital velocity of the first object. Adding the initial and final vectors together, we get a change in speed of twice the orbital velocity of the first body.

No matter how one looks at it, a number like 10 -20 Km/sec in a three body system is huge compared to zero in a two body system. In addition, the one and only inertial reference frame for a gravitational system is the barycenter of the system. In the case of a solar system like ours, said barycenter is very near the center of the Sun. Trying to place a frame of reference near the center of a planet for any trajectory that spans a significant fraction of the radius of the solar system, or even just a few planetary diameters, inevitably results in a non-inertial reference frame, and cannot be accurately matched to real-world mechanics without some seriously complicated math. Newton's law of gravitation considering only the mass of the planet and a small vehicle won't cut it, unless one can live with being up to an order of magnitude off and in completely the wrong direction.

 

[A.T.]

.... a number like 10 -20 Km/sec in a three body system is huge compared to zero in a two body system.

We are moving around the galactic center at 230 km/s. Why is it fine to ignore that?

 

[Filip Larsen]

I have only skimmed the posts in this thread so I might be repeating something already mentioned, but the hyperbolic fly-by of a planet by a probe (the "elastic collision" mentioned above) must be seen from the perspective of the Sun in order to appreciate why it is considered an orbital maneuver relative to the Sun (some actually forgets this), and the fly-by "maneuver" can be conceptually be understood as a rotation of the probes velocity vector relative to the Sun, where the rotation angle is a function by the planet mass and the probes closest distance from it.

Math-wise the whole thing can be modeled fine by a sequence of three two-body problems (Sun orbit before, the hyperbolic fly-by, and Sun orbit after) that are then patched together.

 

[PeroK]

We are moving around the galactic center at 230 km/s, which is even bigger. Why is it fine to ignore that?

Just to add that, AFAIK, the Sun has an almost negligible effect on the orbit of the Moon about the Earth.

We can take the Sun's varying gravity into account for anything and everything. The question is at what point it's necessary for accuracy.

In any case, the concept of gravity assist does not depend on the Sun's varying gravity. Which seems to be what the OP refuses to accept.