Half-face traversal on general polyhedra

[Estanho]

Hi,
I'm developing a data structure to represent 3-D meshes for numeric simulation. I want those meshes to be able to handle any type of polyhedron (not only the classic tetra and hexahedron). The best data structure that I could find was one based on half-edges (or darts), such as this one: https://www.cse.msu.edu/~ytong/papers/halfFace.pdf

The problem is, I want to be able to traverse the faces that compose a given polyhedron, such that this path could be represented as a Hamiltonian cycle on a graph whose nodes are the faces of the polyhedron, and the edges are the face-face connectivity within the polyhedron.

The 2-D counterpart would be a half-edge, which is trivial to traverse as in a Hamiltonian cycle if the graph nodes and edges are the same as the original polygon. All you have to do is follow the half-edges:

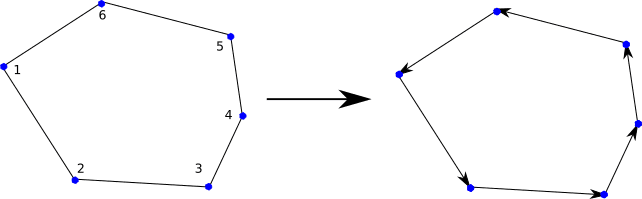
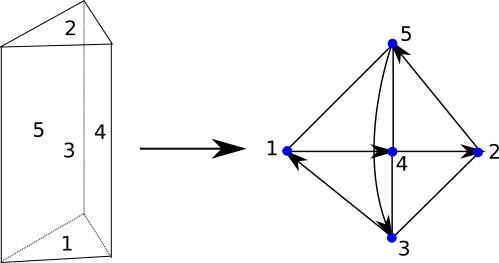
But this doesn't seem to be easy when dealing with faces (or half faces). I don't even know if there will be a hamiltonian path of the faces for every possible polyhedron. And determining those is not easy and hard to keep in memory pre-processed. Here's an example for a prism:

The paper presents a common half-edge, half-face structure to store topological information. This structure allows for some operations (combinatorial maps) on each half-edge: $\beta_1$, $\beta_2$, and $\beta_3$. Those maps are depicted below:

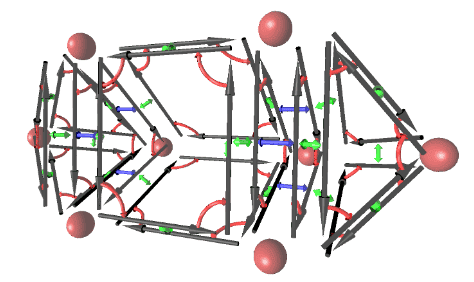
Here, $\beta_1$ is red, $\beta_2$ is green, and $\beta_3$ is blue. So, as you can see, if you apply $\beta_1$ you will get the adjacent half-edge within the same half-face, if you apply $\beta_2$ you will get the adjacent half-edge on an adjacent half-face within the same polyhedron, and if you apply $\beta_3$ you will get the adjacent half-edge on the opposite half-face, from a adjacent polyhedron.

In short, my question is, is there a fast (i.e. with linear complexity) algorithm to traverse all the faces of a given polyhedron using those three operations? It would be sufficient to get just one half-edge for each half-face within the polyhedron, since traversing it is trivial by repeatedly using $\beta_1$.

Until now, it seems my best bet is a graph-search algorithm, which is way too heavy for my needs.

 

[haruspex]

Does Grinberg's Theorem help? https://en.wikipedia.org/wiki/Grinberg's_theorem

 

[Estanho]

Does Grinberg's Theorem help? https://en.wikipedia.org/wiki/Grinberg's_theorem

It could be interesting to proof if all polyhedra contain a hamiltonian cycle on its faces. This theorem can be applied to planar graphs, I'm not sure also if every possible polyhedron can have its faces connectivities mapped to a planar graph. I couldn't think of a counter example, though.

 

[haruspex]

It could be interesting to proof if all polyhedra contain a hamiltonian cycle on its faces. This theorem can be applied to planar graphs, I'm not sure also if every possible polyhedron can have its faces connectivities mapped to a planar graph. I couldn't think of a counter example, though.

Clearly every polyhedron can be flattened out into a planar graph. Just pick one face to be the exterior.
Every 3-connected planar graph can be formed into a polyhedron.

 

[Estanho]

Clearly every polyhedron can be flattened out into a planar graph. Just pick one face to be the exterior.
Every 3-connected planar graph can be formed into a polyhedron.

Oh, of course. I guess I missed my geometry classes.
I will try to work this out. Thanks.

 

[Robert Webb]

Hi, bit late, but couldn't resist commenting on this. I was interested to see Grinberg's theorem, which I wasn't aware of. The wikipedia page shows an example of a non-Hamiltonian graph, so I wondered what this would look like in 3D as a polyhedron. As it happens I wrote a program called Stella4D which can help with this sort of thing. Here's a picture of the model I came up with.

 

[Estanho]

That's cool. If I understand correctly, you wrote a software to convert from a planar graph into a polyhedron? What language did you use?

 

[Robert Webb]

That's cool. If I understand correctly, you wrote a software to convert from a planar graph into a polyhedron? What language did you use?

I wrote a program called Stella4D (http://www.software3d.com/Stella.php) for investigating polyhedra and 4D polytopes (it's commercial software FYI). It has a little-known feature to build new polyhedra using a spring-relaxation system, from a description of its topology alone. I used it originally to generate many of Stella's built-in polyhedra, such as the Johnson solids and near misses. You specify all the faces, based on vertex indices (which you assign arbitrarily), which can be a bit tedious, but it's good for things that can't easily be made other ways. In fact I just created a better realisation of the above non-Hamiltonian graph. This one has all regular 9-gons and 8-gons. Only the pentagons remain irregular:

Here's the input I used for Stella4D:

h ~6 (0 1 2 3 4 5 6 7 8)
(9 26 41 42 43 44 27 10)
(21 20 35 36 37 38 39 22)
(15 14 29 30 31 32 33 16)
(0 8 25 26 9) (8 7 23 24 25) (7 6 21 22 23)
(6 5 19 20 21) (5 4 17 18 19) (4 3 15 16 17)
(3 2 13 14 15) (2 1 11 12 13) (1 0 9 10 11)
(25 24 40 41 26) (23 22 39 40 24)
(19 18 34 35 20) (17 16 33 34 18)
(13 12 28 29 14) (11 10 27 28 12)
(40 39 38 42 41) (34 33 32 36 35) (28 27 44 30 29)
(45 43 42 38 37) (45 37 36 32 31) (45 31 30 44 43)

The "h" means the model is convex, so an initial parse is done where extra springs are used to expand the graph like a balloon.
The "~6" means that all faces with 6 or less sides are irregular, so in this case the 8- and 9-gons are made regular.
Each face is define inside parentheses. The vertex indices can be seen below:

Stella4D can also print out unfolded nets to cut out and glue together, so I might make one in paper. It's an interesting polyhedron.

Oh, and Stella4D was written in C++ using OpenGL for graphics.

 

[Estanho]

Got it. Nice piece of software, congratulations. I don't have dollars to spare right now since I'm a mere MSc student but I might look forward to buying it in the future.

 

[Estanho]

Also, your work reminds me of one other from a professor of my local University. He works with these so-called UNIVs, which are sculptures representing seven-dimensional spaces.
You can see his phd thesis here: https://arxiv.org/pdf/math/0305058.pdf