Hello HelloWorld,
First, we should observe that since there is cyclic symmetry between the variables, we should expect to get the same result revolving about either axis, however, I will work through both parts of the problem as if we do not know this. Also, I will use both the shell and washer methods, to demonstrate both methods, and as a check.
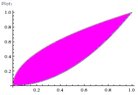
First, let's draw a diagram of the region to be revolved:
View attachment 1334
a) Revolving about the $x$-axis, using the shell method, we find the volume of an arbitrary shell is:
$$dV=2\pi rh\,dy$$
where:
$$r=y$$
$$h=\sqrt{y}-y^2=y^{\frac{1}{2}}-y^2$$
And so we have:
$$dV=2\pi y\left(y^{\frac{1}{2}}-y^2 \right)\,dy=2\pi \left(y^{\frac{3}{2}}-y^3 \right)\,dy$$
Summing the shells by integrating, we first determine the limits of integration. If we square the equation $x=y^2$ to get $x^2=y^4$, then equate the two expressions for $x^2$, we find:
$$y=y^4$$
$$y\left(1-y^3 \right)=0$$
$$y(1-y)\left(1+y+y^2 \right)=0$$
The two real roots are:
$$y=0,\,1$$
Which means the two curves intersect at the points $(0,0),\,(1,1)$.
Hence, we may find the volume with:
$$V=2\pi\int_0^1 y^{\frac{3}{2}}-y^3\,dy$$
Applying the FTOC, we have:
$$V=2\pi\left[\frac{2}{5}y^{\frac{5}{2}}-\frac{1}{4}y^4 \right]_0^1=2\pi\left(\frac{2}{5}-\frac{1}{4} \right)=\frac{3\pi}{10}$$
Now, let's check this by using the washer method. The volume of an arbitrary washer is:
$$dV=\pi\left(R^2-r^2 \right)\,dx$$
where:
$$R=\sqrt{x}$$
$$r=x^2$$
and so we have:
$$dV=\pi\left(\left(\sqrt{x} \right)^2-\left(x^2 \right)^2 \right)\,dx=\pi\left(x-x^4 \right)\,dx$$
Summing the washers, we find:
$$V=pi\int_0^1 x-x^4\,dx$$
Applying the FTOC, we find:
$$V=\pi\left[\frac{1}{2}x^2-\frac{1}{5}x^5 \right]_0^1=\pi\left(\frac{1}{2}-\frac{1}{5} \right)=\frac{3\pi}{10}$$
And this checks with the result from the shell method.
b) Revolving about the $y$-axis, using the shell method, we find the volume of an arbitrary shell is:
$$dV=2\pi rh\,dx$$
where:
$$r=x$$
$$h=\sqrt{x}-x^2=x^{\frac{1}{2}}-x^2$$
And so we have:
$$dV=2\pi x\left(x^{\frac{1}{2}}-x^2 \right)\,dy=2\pi \left(x^{\frac{3}{2}}-x^3 \right)\,dx$$
Since we will integrate from $x=0$ to $x=1$ it now becomes obvious that we will get the same volume as in part a).