beh4R
- 3
- 0
Hello .
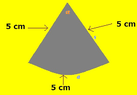
I am in the end of my exams and i have to do a geometry figure like a pyramid ( view image ) below
Now i should find the Perimeter, Volume and Surface of this figure .
Lengths are all 5 cm, Can somebody find and write the
Permiter,volume and surface for this figure please it's urgent


I am in the end of my exams and i have to do a geometry figure like a pyramid ( view image ) below
Now i should find the Perimeter, Volume and Surface of this figure .
Lengths are all 5 cm, Can somebody find and write the
Permiter,volume and surface for this figure please it's urgent