How can I find the CDF and PDF of Y?

[Jonobro]

Problem

Let X be a uniform(0,1) random variable, and let Y=e^−X.
Find the CDF of Y.
Find the PDF of Y.
Find EY.

Relevant Equations

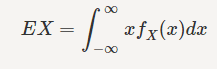
http://puu.sh/kAVJ8/0f2b1e7b22.png

My attempt at a solution

If I solve for the range of y I get (1, 1/e), but because Y is not an increasing function, my second bound is smaller than my first. I am really confused as to how I would be able to solve for the CDF and PDF in this case... Any help would be greatly appreciated.

 

[RUber]

https://www.physicsforums.com/threa...ction-of-a-continuous-random-variable.836066/

 

[mathman]

To get CDF:
P(Y<y)=P(e^{-X}<y)=P(-X<lny)=P(X\ge -lny)=1+lny
PDF = \frac{1}{y}

 

[Jonobro]

This is very helpful. Thanks. However, would the CDF be 0 for y < 1 and 1 for y > 1/e? This part does not really make sense.

 

[RUber]

Mathman's formula is pretty clear for the cdf. It is equal to 0 at y=1/e, and 1 at y=1, and increasing in between.

 

[gill1109]

Mathman's formula is pretty clear for the cdf. It is equal to 0 at y=1/e, and 1 at y=1, and increasing in between.

... which is just what we expect since X certainly lies between 0 and 1, hence Y = exp(-X) lies between 1/e and 1. The density of Y is zero left of 1/e and right of 1. And in between it's the derivative of mathman's cumulative distribution function, hence 1/y.

Check: 1/y integrates to 1 when you integrate it from 1/e to 1