- #1
utp9
- 12
- 2
- TL;DR Summary
- Solve an equation of power through a linear graph.
I am doing an investigation of how much a beam sags, based on the distance from its midpoint.
This is my hypothetical equation:
The relationship between distance, d and sag, s is not a linear relationship. Below, is the determined relationship between the variables, linearized by natural logarithm.[1]
\begin{align*}
s &∝ d^t & \quad &s = \text{vertical sag(mm)}\\
s &= ud^t &\text{(equation one)}\quad &d = \text{distance(mm)}\\
\ln(s) &= \ln(ud^t) & \quad &u = \text{constant}\\
\ln(s) &= t\ln(d) + \ln(u) &\text{(equation two)} \quad & t = \text{constant}\\
\end{align*}
These are my data points:
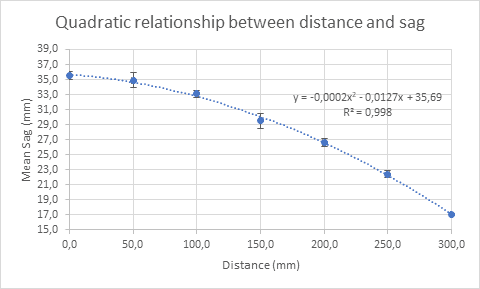
I get this polynomial(to the second degree) of these points:
Applying ln-ln to the x and y-axis gets me these data points:
*As ln(0) is not a real number, the distance 0.0mm will not be included in the graph
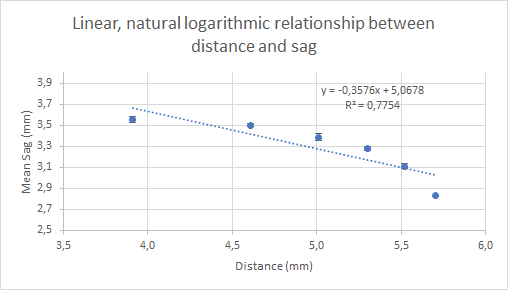
My "linear" graph looks like this:
With the graph, ln(u) is my y-intercept and t is my gradient to complete the equation in my hypothesis.
My question:
I cannot figure out what is going wrong as everything should work in this situation. I have 10 pages of report ready except for this last graph and conclusion based off the graph.
I've spent hours yesterday attempting to understand what is going wrong, if anyone can help or needs more information please comment.
[1] “Getting Straight Line Graphs.” Physics for the IB Diploma Exam Preparation Guide, by K. A. Tsokos, Cambridge University Press, 2016, p. 5.
This is my hypothetical equation:
The relationship between distance, d and sag, s is not a linear relationship. Below, is the determined relationship between the variables, linearized by natural logarithm.[1]
\begin{align*}
s &∝ d^t & \quad &s = \text{vertical sag(mm)}\\
s &= ud^t &\text{(equation one)}\quad &d = \text{distance(mm)}\\
\ln(s) &= \ln(ud^t) & \quad &u = \text{constant}\\
\ln(s) &= t\ln(d) + \ln(u) &\text{(equation two)} \quad & t = \text{constant}\\
\end{align*}
These are my data points:
| Sag of the beam s / mm ∆mm = ±1.0 | | |||
Distance d / mm ∆mm = ±0.5 | Trial 1 | Trial 2 | Trial 3 | Trial 4 | Mean sag s / mm |
0.0 | 35.0 | 36.0 | 36.0 | 35.0 | 35.5 ±0.5 |
50.0 | 34.0 | 36.0 | 35.0 | 34.5 | 34.9 ±1.0 |
100.0 | 32.5 | 33.0 | 33.5 | 33.5 | 33.1 ±0.5 |
150.0 | 29.0 | 30.0 | 30.0 | 29.0 | 29.5 ±1.0 |
200.0 | 26.0 | 27.0 | 26.5 | 27.0 | 26.6 ±0.5 |
250.0 | 22.0 | 23.0 | 22.0 | 22.5 | 22.4 ±0.5 |
300.0 | 17.0 | 17.0 | 17.0 | 17.0 | 17.0 ±0.0 |
I get this polynomial(to the second degree) of these points:
Applying ln-ln to the x and y-axis gets me these data points:
Distance d / mm ∆mm = ±0.5 | Ln(d) | Mean sag s / mm | Ln(s) |
0.0 | UND* | 35.5 ±0.5 | 3.6 ±0.0 |
50.0 | 3,9 | 34.9 ±1.0 | 3.6 ±0.0 |
100.0 | 4,6 | 33.1 ±0.5 | 3.5 ±0.0 |
150.0 | 5,0 | 29.5 ±1.0 | 3.4 ±0.0 |
200.0 | 5,3 | 26.6 ±0.5 | 3.3 ±0.0 |
250.0 | 5,5 | 22.4 ±0.5 | 3.1 ±0.0 |
300.0 | 5,7 | 17.0 ±0.0 | 2.8 ±0.0 |
My "linear" graph looks like this:
With the graph, ln(u) is my y-intercept and t is my gradient to complete the equation in my hypothesis.
My question:
I cannot figure out what is going wrong as everything should work in this situation. I have 10 pages of report ready except for this last graph and conclusion based off the graph.
I've spent hours yesterday attempting to understand what is going wrong, if anyone can help or needs more information please comment.
[1] “Getting Straight Line Graphs.” Physics for the IB Diploma Exam Preparation Guide, by K. A. Tsokos, Cambridge University Press, 2016, p. 5.
Last edited:
