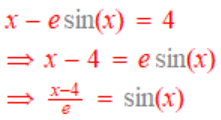SUMMARY
The equation x - e*sin(x) = 4 does not have a closed-form solution, as confirmed by the discussion participants. Instead, solutions can be expressed using special functions like the Lambert W function, which allows for implicit representation rather than explicit solutions. While some equations, such as x + 3*sin(x) = 0, may yield trivial solutions, this is not applicable to all similar equations. Historical attempts by mathematicians like Newton highlight the complexity of finding solutions to such transcendental equations.
PREREQUISITES
- Understanding of transcendental equations
- Familiarity with the Lambert W function
- Basic knowledge of numerical methods for root-finding
- Concept of Euler's number (e) and its applications
NEXT STEPS
- Research the properties and applications of the Lambert W function
- Learn about numerical methods such as Newton's method for solving equations
- Explore transcendental equations and their characteristics
- Study examples of equations with known analytic solutions
USEFUL FOR
Mathematicians, students studying calculus or numerical analysis, and anyone interested in solving complex equations involving transcendental functions.