Discussion Overview
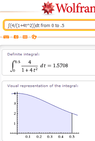
The discussion revolves around the integration of the function $\displaystyle\int_0^\frac{1}{2}\frac{4}{1-4t^2}dt$ and the challenges participants face in solving it. The conversation includes various methods of integration, including the log rule, partial fraction decomposition, and the Heaviside cover-up method, as well as the implications of typos in mathematical expressions.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant initially attempts to use the log rule for integration but expresses uncertainty about its applicability due to the form of the integrand.
- Another participant suggests using partial fraction decomposition, indicating that the Heaviside cover-up method could be effective.
- Some participants assert that the integral diverges based on the original expression provided, while others question the correctness of the setup.
- There are discussions about the necessity of breaking down the integrand into simpler fractions and the challenges associated with finding coefficients in partial fractions.
- One participant mentions that the integral may require the use of the inverse tangent function, suggesting a different approach altogether.
- Several participants share formulas related to integration that they believe are not commonly taught, sparking a debate about teaching methods and memorization versus understanding.
- There are expressions of confusion and fatigue from participants, indicating the complexity of the problem and the various methods being discussed.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the best method to solve the integral, with multiple competing views on the appropriate approach and the validity of the original integral. Some assert that the integral diverges, while others propose methods that may lead to a solution.
Contextual Notes
Participants note that the integral as presented may contain a typo, leading to confusion about its convergence. There are also references to different methods of integration that may not be universally taught, which could affect participants' approaches to the problem.
Who May Find This Useful
This discussion may be of interest to students and educators in calculus, particularly those exploring integration techniques and the importance of precision in mathematical expressions.