How Do You Describe an Equivalence Class?

[andrew1]

Hi,

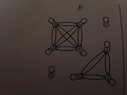
I'm having trouble understanding the concept of equivalence classes and would like some help on what it means to describe an equivalence class.

Here is an example that I have deemed to be an equivalence relation but I have no idea about how I can descrive its equivalence class

View attachment 2405

 

[Evgeny.Makarov]

An equivalence class is a group of nodes such that one can travel from one node of the group to any other node of the group along the arrows. So this relation has four equivalence classes.

It's not hard to see that since this is an equivalence relation, one can travel from node $a$ to node $b$ in several steps iff one can travel from $a$ to $b$ in just one step.

 

[Opalg]

An equivalence relation on a set has the effect of splitting the set into a collections of subsets (called equivalence classes). Within each equivalence class all the elements of that class are related to each other. But elements of different equivalence classes are not related. In your diagram the equivalence relation on the set $E$ splits it into four equivalence classes, namely $\{a,b,d,e\}$, $\{c\}$, $\{g\}$ and $\{f,h,i\}.$

 

[andrew1]

Thanks guys, that sounds much simpler than my notes.

 

[blue_raver22]

.

Equivalence classes are a mathematical concept used to group objects or elements that are considered equivalent in some way. In other words, an equivalence class is a set of objects that are related to each other through a certain equivalence relation.

In your example, you have determined that there is an equivalence relation present. This means that there is a relationship between the objects in the set that satisfies the properties of reflexivity, symmetry, and transitivity. In order to describe the equivalence class, you need to first identify the equivalence relation and then determine the objects that are related to each other through this relation.

For example, if the equivalence relation is "having the same color", then the equivalence class would be all the objects that have the same color. If the equivalence relation is "being a multiple of 3", then the equivalence class would be all the objects that are multiples of 3. In other words, the equivalence class is the set of all objects that are related to each other through the defined equivalence relation.

It is important to note that there can be multiple equivalence classes within a set, depending on the chosen equivalence relation. So, in order to describe an equivalence class, you need to specify the equivalence relation that is being used.

I hope this helps clarify the concept of equivalence classes. If you have any further questions, please let me know.