How Do You Minimize Mean Square Deviation in Dice Roll Predictions?

[mathmari]

Hey! :giggle:

We consider a double roll of the dice. The random variable X describes the number of pips in the first roll of the dice and Y the maximum of the two numbers.
The joint distribution and the marginal distributions are given by the following table

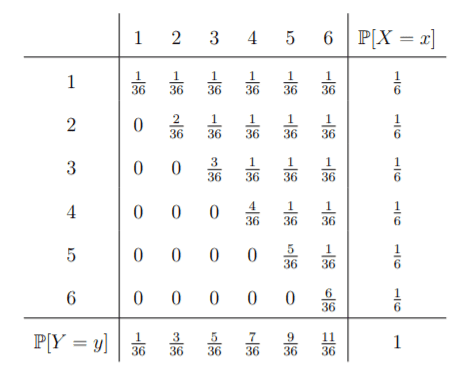
Using :
For all $a,b\in \mathbb{R}$ it holds that $$E[(Y-a-bX)^2]\geq E[(Y-a^{\star}-b^{\star}X)^2]=Var(Y)(1-\rho^2(X,Y))$$ where $b^{\star}=\frac{Cov(X,Y)}{Var(X)}$ and $a^{\star}=E[Y-b^{\star}X]$.

Determine $a,b\in \mathbb{R}$ such that for X and Y the mean square deviation $E [(Y - (a + bX))^2]$ becomes minimal. Give also the corresponding minimum value for this mean square deviation.This term is minimal when $b=\frac{Cov(X,Y)}{Var(X)}$ and $a=E[Y-b^{\star}X]$, right? Sowe have to calculate these values, don't we? :unsure:

 

[I like Serena]

Hey mathmari!

Yep. (Nod)

 

[mathmari]

Yep. (Nod)

We have that $\text{Cov}(X,Y)=E[XY]-E[X]E[Y]$ with \begin{align*}E[XY]&=\sum_{x}\sum_{y}xyP[X=x,Y=y]\\ & =1\cdot 1\cdot \frac{1}{36}+1\cdot 2\cdot \frac{1}{36}+1\cdot 3\cdot \frac{1}{36}+1\cdot 4\cdot \frac{1}{36}+1\cdot 5\cdot \frac{1}{36}+1\cdot 6\cdot \frac{1}{36} \\ & +
2\cdot 2\cdot \frac{2}{36}+2\cdot 3\cdot \frac{1}{36}+2\cdot 4\cdot \frac{1}{36}+2\cdot 5\cdot \frac{1}{36}+2\cdot 6\cdot \frac{1}{36}\\ & +
3\cdot 3\cdot \frac{3}{36}+3\cdot 4\cdot \frac{1}{36}+3\cdot 5\cdot \frac{1}{36}+3\cdot 6\cdot \frac{1}{36} \\ & +
4\cdot 4\cdot \frac{4}{36}+4\cdot 5\cdot \frac{1}{36}+4\cdot 6\cdot \frac{1}{36} \\ & +
5\cdot 5\cdot \frac{5}{36}+5\cdot 6\cdot \frac{1}{36}\\ & +
6\cdot 6\cdot \frac{6}{36}
\\ & =\frac{7}{12} +\frac{11}{9} + 2+ 3 + \frac{155}{36} + 6\\ & =\frac{154}{9}
\end{align*} and \begin{align*}&E[X]=\sum_xxP[X=x]=1\cdot \frac{1}{6}+2\cdot \frac{1}{6}+3\cdot \frac{1}{6}+4\cdot \frac{1}{6}+5\cdot \frac{1}{6}+6\cdot \frac{1}{6}=\frac{7}{2}\\ &E[Y]=\sum_yyP[Y=y]=1\cdot \frac{1}{36}+2\cdot \frac{3}{36}+3\cdot \frac{5}{36}+4\cdot \frac{7}{36}+5\cdot \frac{9}{36}+6\cdot \frac{11}{36}=\frac{161}{36}\end{align*}
So we get $\text{Cov}(X,Y)=E[XY]-E[X]E[Y]=\frac{154}{9}-\frac{7}{2}\cdot \frac{161}{36}=\frac{35}{24}$.

The variance is equal to \begin{align*}Var(X)&=E[X^2]-(E[X])^2=\sum_xx^2P[X=x]-\left (\frac{7}{2}\right )^2\\ & =\left (1^2\cdot \frac{1}{6}+2^2\cdot \frac{1}{6}+3^2\cdot \frac{1}{6}+4^2\cdot \frac{1}{6}+5^2\cdot \frac{1}{6}+6^2\cdot \frac{1}{6}\right )-\frac{49}{4}=\frac{91}{6}-\frac{49}{4}\\ & =\frac{35}{12}\end{align*}

Therefore we get \begin{equation*}b^{\star}=\frac{Cov(X,Y)}{Var(X)}=\frac{\frac{35}{24}}{\frac{35}{12}}=\frac{1}{2}\end{equation*} For $a$ we have that \begin{equation*}a^{\star}=E[Y-b^{\star}X]=E\left [Y-\frac{1}{2}X\right ]=E[Y]-\frac{1}{2}\cdot E[X]=\frac{161}{36}-\frac{1}{2}\cdot \frac{7}{2}=\frac{49}{18}\end{equation*}

Is everything correct and complete? :unsure:

 

[mathmari]

So the minimal value is
\begin{align*}E[(Y -(a^{\star}+b^{\star}X))^2]&=E\left [\left (Y -\left (\frac{49}{18}+\frac{1}{2}X\right )\right )^2\right ]\\ & =E\left [\frac{2401}{324} + \frac{49}{18} X + \frac{1}{4}X^2 - \frac{49}{9} Y - X Y + Y^2\right ]\\ & =\frac{2401}{324} + \frac{49}{18} E[X] + \frac{1}{4}E[X^2] - \frac{49}{9} E[Y ]- E[X Y] + E[Y^2]\\ & =\frac{2401}{324} + \frac{49}{18} \cdot \frac{7}{2} + \frac{1}{4}\cdot \frac{91}{6} - \frac{49}{9}\cdot \frac{161}{36}- \frac{154}{9} + E[Y^2]\\ & =-\frac{13433}{648} + E[Y^2]\end{align*}
We have that \begin{equation*}E[Y]=\sum_yy^2P[Y=y]=1^2\cdot \frac{1}{36}+2^2\cdot \frac{3}{36}+3^2\cdot \frac{5}{36}+4^2\cdot \frac{7}{36}+5^2\cdot \frac{9}{36}+6^2\cdot \frac{11}{36}=\frac{791}{36}\end{equation*}
Therefore we get \begin{equation*}E[(Y -(a^{\star}+b^{\star}X))^2]=-\frac{13433}{648} + \frac{791}{36}=\frac{805}{648}\end{equation*}
Is that correct ? :unsure:

 

[I like Serena]

Typically we should check whether what we found "makes sense".
In the case of a least squares approximation, we usually draw a graph to see if the line we found matches the points more or less.
A graph also serves to see if it even makes sense to apply a least square approximation.

In this case we can also look at the numbers.
We found the minimal relation $\hat Y=a^*+b^*X=\frac{49}{18} + \frac 12 X$.
For $X=1$ we have equal probabilities for each of the possible $Y$, so we expect a result where $\hat Y$ is in the middle between 3 and 4.
If we fill it in, we get $\hat Y(1)=\frac{49}{18}+\frac 12\cdot 1\approx 3.22$, so that is in the right neighborhood.
We should do the same thing for at least $X=6$ where we expect $\hat Y\approx 6$.