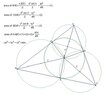
SUMMARY
The incenter \( I \) of triangle \( ABC \) is defined as the point where the angle bisectors of the triangle intersect. Given the side lengths \( BC = a \), \( AC = b \), and \( AB = c \), the distances from the incenter to the vertices are denoted as \( IA = x \), \( IB = y \), and \( IC = z \). The relationship \( ax^2 + by^2 + cz^2 = abc \) is established as a key property of the incenter in relation to the triangle's side lengths.
PREREQUISITES
- Understanding of triangle geometry and properties
- Familiarity with angle bisectors and incenters
- Knowledge of algebraic manipulation and proof techniques
- Basic concepts of Euclidean geometry
NEXT STEPS
- Study the properties of triangle centers, focusing on incenters and circumcenters
- Explore proofs involving triangle inequalities and their implications
- Learn about the relationship between triangle area and side lengths
- Investigate advanced geometric theorems related to triangle centers
USEFUL FOR
Mathematicians, geometry enthusiasts, and students studying triangle properties and proofs will benefit from this discussion.