How Far Can Chris Walk on a Cantilevered Beam Without Tipping?

[TheKovac]

Homework Statement

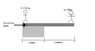
Chris and Robin use a 3m, 40kg, plank to span 2m over a river. The plank is set up with 1.0m on the bank and Robin is standing so that her centre of mass is 0.2m from the end. The diagram attached shows Chris (50kg) walking out on the plank. Robin has a mass of 80kg.

How far can Chris safely walk from the bank?

Homework Equations

t = Fd
W= mg

The Attempt at a Solution

T(robin) = T(chris)
(50*9.80)r = (80*9.8)(2)
r = 3.2 m ??

I can't seem to see any other way of working the answer out? CAN someone please give me a push in the right direction?

Kindest Regards,
TheKovac

 

[alphysicist]

Hi TheKovac,

What pivot point have you chosen for this problem? To find the best one, think what the plank will be doing when Chris is just barely on the verge of going too far.

At that point, there will be four forces acting on the plank, so you'll need to have at least three in your torque equation.

 

[TheKovac]

Hi TheKovac,

What pivot point have you chosen for this problem? To find the best one, think what the plank will be doing when Chris is just barely on the verge of going too far.

At that point, there will be four forces acting on the plank, so you'll need to have at least three in your torque equation.

Well I believe there are two force in an upward direction, and then one force of Weight going in a downward direction.

Am I right?

So the next step for me, is to work out the two opposing forces?

 

[alphysicist]

I think there are three forces in the downward direction acting on the plank (the weight of the two people and the weight of the plank itself), and there is one force upward (the normal force from the ground).

You have to locate where these are located at when the plank is just on the verge of tipping. (Of course the location of Chris is an unknown, but you can tell what region it's into draw it on a diagram; you can find out exactly where the other three forces are.) Once you have the four locations, you can pick the best pivot point and write the torque equation to get the answer.

 

[TheKovac]

So I figure these are the following forces. (see diagram)

Therefore, I believe I should create my equation based upon the middle force, right at the edge of the support - is that correct?

 

[alphysicist]

Well, I've heard it can take at least several hours before your attachment is approved and I can see it. But it sounds like you are saying to place the pivot right at the end of the ground (1 meter from the end where the ground meets the river). That's right; that is where the unknown normal force is acting, so by placing the pivot there that unknown will not be in the equation. (Although in this case, it's very easy to find the value of the normal force.) With that choice, what is your torque equation?

 

[luben]

Hi Kovac, you can consider sharing the picture through tinypic.com or other photo shareing sites you preferred. this does not require approval. probably speed up our progress. cannot wait to see it

 

[TheKovac]

So therefore, the equation for the pivot and the torque would be:

T(robin) = T(chris)
(2* (9.8*80) - (1*(9.8*50) = r

IS that Right?

 

[alphysicist]

No, I don't believe that's right. The full equilibrium condition would be:

T(robin) + T(chris)+ T(board weight) + T (normal force) = 0

(some of the torques are negative). Because you put the pivot point right at the normal force (where the ground and water area meet, 1 meter from the left end), then T(normal force)=0.

You still have to account for the torque from the weight of the plank, so your equation needs three terms.




Looking at your last post, you had that the torque from robin (80 kg) is:

T(robin) = 2 * (9.8 * 8))

that's really close, except robin is not 2 meters from the pivot point. How far is the distance?

For the torque from chris (50 kg), you have:

T(chris) = - 1 * (9.8 * 50)

you have the correct sign; the only problem is the distance. We don't know that Chris is 1 meter from the pivot; that distance is what we are trying to find, so call it x.

Once you correct those two terms and include the torque from the weight of the board, you should be able to solve for x. What do you get for your torque equation?