- #1
How is this equality possible? What did the professor do to reach it?
- Thread starter tahlaskerssen
- Start date
-
- Tags
- Professor
In summary, the conversation discusses the process of factoring sums in an expression involving a long summation and common terms. It explains how to combine two summations into one and simplify the expression to make it less intimidating. The speaker also expresses their surprise at not knowing this technique and thanks the other person for their help.
- #2
NascentOxygen
Staff Emeritus
Science Advisor
- 9,242
- 1,074
tahlaskerssen said: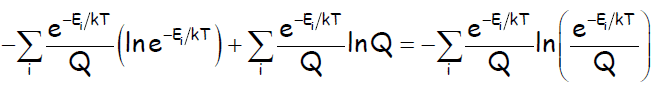
Can someone explain me how one term got to the other term? It makes no sense to me
Your image is not publicly accessible. Can you change its permissons?
- #3
tahlaskerssen
- 10
- 0
NascentOxygen said:
I uploaded it.
By the way, he said something about "factoring sums out" what is that supposed to mean? This is the first time I've ever encountered something like this and i have taken up to differential equations regarding my math level.
- #4
NascentOxygen
Staff Emeritus
Science Advisor
- 9,242
- 1,074
The expression is of the form: A. ln Q - A. ln w
where A is a long summation and common to both terms.
Besides A, ln Q is the other term inside the first summation (likewise, besides A, you can see that ln w is the other term in the second series).
As each summation is over the same range, then you can combine the two series in one, using just one sigma.
Then combine the terms into one making use of: ln Q - ln w = ln (Q/w)
finally remember: ln (Q/w) = - ln (w/Q)
It looks forbidding, but really isn't.
Basically, write the expression without the ∑ symbol, and simplify what you see.
EDITED
where A is a long summation and common to both terms.
Besides A, ln Q is the other term inside the first summation (likewise, besides A, you can see that ln w is the other term in the second series).
As each summation is over the same range, then you can combine the two series in one, using just one sigma.
Then combine the terms into one making use of: ln Q - ln w = ln (Q/w)
finally remember: ln (Q/w) = - ln (w/Q)
It looks forbidding, but really isn't.
Basically, write the expression without the ∑ symbol, and simplify what you see.
EDITED
Last edited:
- #5
tahlaskerssen
- 10
- 0
i'm so stupid.. i deserve to go start college again.. Thanks a lot man!(honestly, i didnt know you could combine two same series into one, i was just treating them as a normal number and they were cancelling each other or getting a sigma squared, lol)
FAQ: How is this equality possible? What did the professor do to reach it?
1. How is this equality possible?
This equality is possible through a series of mathematical equations and calculations that have been rigorously tested and proven to be accurate.
2. What did the professor do to reach it?
The professor likely used their knowledge of the subject and applied various mathematical principles and techniques to derive this equality. They may have also conducted experiments or gathered data to support their findings.
3. How can we be sure that this equality is accurate?
The accuracy of this equality can be confirmed through peer review by other scientists and by replicating the results through experimentation and further analysis.
4. Are there any limitations to this equality?
As with any scientific discovery, there may be limitations or exceptions to this equality that have not yet been discovered or explored. Further research and testing may reveal additional factors or variables that could affect its validity.
5. Can this equality be applied to other situations or scenarios?
It is possible that this equality can be applied to similar situations or scenarios, but it is important to consider the specific variables and conditions that were used to reach this equality. Further research and analysis may be needed to determine its applicability in other contexts.