How Much Work Does Ryan Do Lifting and Carrying Potatoes?

[LonelyElectron]

Hey all! I have three questions below and was hoping someone could proof read, and offer some guidance for the last one... Any help is greatly appreciated!

Question 1:
1. Homework Statement
Ryan needs to carry a bag of potatoes to the car. Determine how much work Ryan has to do to lift a 20 kg bag of potatoes to his shoulder, 1.7 m above the floor, and how much work he does as he carries this bag of potatoes to his car, which is parked 45 m away? Show your work.

Homework Equations

F_g = mg
W = Fd

The Attempt at a Solution

Question 2:

Homework Statement

For a 1480 kg car that accelerates uniformly from a position of rest to a speed of 95 km/h in 6.0 s:
-calculate the car's acceleration
-determine how far the car traveled during this acceleration
-determine how much work was done by the car during this 6.0 s
-identify what power was developed during this process

Homework Equations

F=ma
W=fd
v_f = v_i +at
d=1/2(v_i + v_f)t
P=W/t

The Attempt at a Solution

Question 3:

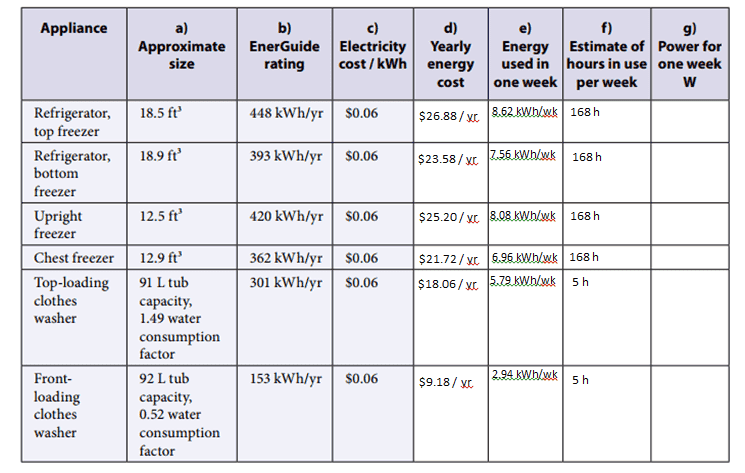
Homework Statement

​

Fill in the empty columns of the following table.​

​

Homework Equations

​

No idea. I used common sense.​

​

The Attempt at a Solution

​

​

very lost as to how I can fill out the last column... ​

 

[kuruman]

Power is expressed in Watts or Joules/s. It is the rate at which energy is generated or dissipated. In short, divide energy by time and you have power. Mind your units. Also, for future reference, please post unrelated questions on separate threads.

 

[phinds]

very lost as to how I can fill out the last column...

Well, you have kilowatt-hours per week. What is the relationship between kilowatt-hours and work?

 

[phyzguy]

Question 1 looks good.
Question 2, you did the first two right, but then when calculating the work you multiplied by the distance instead of the acceleration. So your calculation of the work done and the power are both wrong.

In the last column of the table, you have how much energy is used in one week. Since power is energy/time, you just need to divide the energy used in one week by the number of hours in a week.

 

[LonelyElectron]

Oh wow... Thanks for the fast replies! Okay, so for question 3, the power is the energy over time. I did the first question in the table and got P=8.62/168=0.051. That's kW because I had kWh as my power, right? So to make it into watts for the answer, I multiply by 1000, which gives me 51 W. Is that correct? As long as the process is right I think I can confidently get the rest :)

As for question 2, I am a little confused by the need for acceleration? The only equation I have been given for work thus far is W=Fd, or W =mgd. Am I missing something?

 

[kuruman]

As for question 2, I am a little confused by the need for acceleration?

In question 2 you say F = ma but you multiply the mass by the 79.17 which is the number for the distance traveled, not the acceleration.

On edit: kW h/week is not an energy unit; kW h is.

 

[LonelyElectron]

In question 2 you say F = ma but you multiply the mass by the 79.17 which is the number for the distance traveled, not the acceleration.

On edit: kW h/week is not an energy unit; kW h is.

Brilliant on your part! I can't believe I switched my values like that in number 2... Here is the updated. Look better?

As for kWh, not sure I understand. Physics doesn't seem to be my forte...

 

[kuruman]

Problem 2 agrees with my numbers. To complete the picture, note that you didn't have to go through the acceleration to get the answer. I the car acquires kinetic energy K = ½mv² in time t, then the average power is P = (½mv²)/t. You get the same number.

As for kWh, not sure I understand. Physics doesn't seem to be my forte...

You don't really need to understand physics in order to understand kWh. If you understand money, it's enough. Say your weekly salary is $1,000.00. That's a rate of 1 k$/week. If someone asked you how much you make in a month, you would multiply the rate by the number of weeks in a month (= 4) and say (1 k$/week)*4 (week) = 4 k$. If, instead, you were asked how much you make in one working hour (1/40 of a working week), you would say (1 k$/week)*(1/40) week= 0.025 k$. Same thing with kW. The kWh is the amount of energy generated/consumed in one hour. It's an energy and therefore can be expressed in Joules by noting that there are 3600 seconds in one hour. Thus, 1 KWh = 1000 Wh =1000 (J/s)h = 1000(J/s)3600s = 3.6×10⁶ J = 3.6 MJ. So the energy cost of $0.06 per kWh means that one is paying only 6 cents to buy 3.6 million Joules or 600,000 J for a penny. What a deal!