How to compute the following set of ODEs with ICs

[JD_PM]

TL;DR

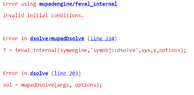
I am trying to solve the following set of 5 first order ODEs with ICs but I get an error output "invalid ICs". What am I missing?

I am trying to solve the following set of 5 first order ODEs

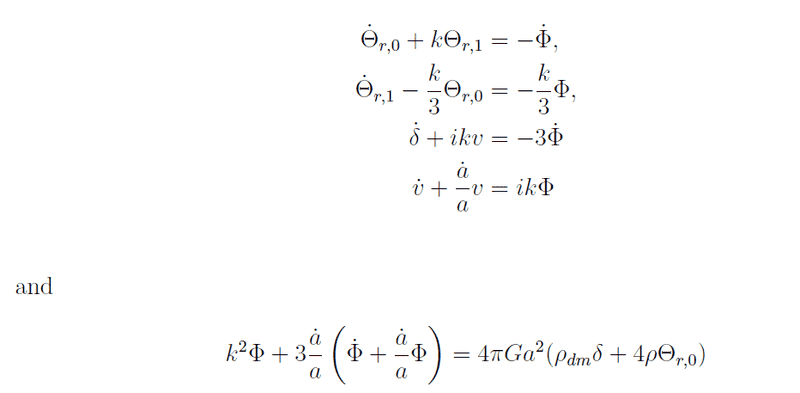
Where the variables are $\Theta_0, \Theta_1, \Phi, \delta$ and $v$. The initial conditions (ICs) are

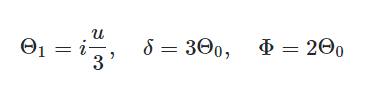
(Note that there is a typo in the above ICs; it is $v$ instead of $u$). I am following this solved sample, following the exact same steps. However I get an error

Are these 3 ICs not enough?

Thank you!

 

[phyzguy]

Your notation isn't clear, at least not to me. If \Theta_{0} and \Theta_{1} are the variables, what are \Theta_{r,0} and \Theta_{r,1}? Also, isn't a a variable as well? There is an \dot{a} term.

 

[JD_PM]

Sorry, let me clarify

Your notation isn't clear, at least not to me. If \Theta_{0} and \Theta_{1} are the variables, what are \Theta_{r,0} and \Theta_{r,1}?

I dropped the subscript $r$. For our purpose, we can simply work with $\Theta_{0}$ and $\Theta_{1}$.

Also, isn't a a variable as well? There is an \dot{a} term.

Right but let us assume that the $a$ function barely changes w.r.t. time, so that $\dot a$ is a constant

 

[phyzguy]

OK. Then I have one question and one suggestion. Your initial conditions are written as though they are true for all values of t (I'm assuming the independent variable is t). Is this right, or are they only true at t=0? If they are only true at t=0, did you specify it this way when you entered it into the code? It would be easier for us to understand if you share the code you entered. As for the suggestion, why not use the first two equations to eliminate \Phi as a variable and get down to just four variables?

 

[JD_PM]

OK. Then I have one question and one suggestion. Your initial conditions are written as though they are true for all values of t (I'm assuming the independent variable is t). Is this right, or are they only true at t=0? If they are only true at t=0, did you specify it this way when you entered it into the code? It would be easier for us to understand if you share the code you entered.

I worked with ICs at $t=0$. Let me share the code

syms u(t) v(t) w(t) x(t) y(t) a b d G k %Note that u corresponds to the variable v (see #1), v to \delta, w to \Theta_0, x to \Theta_1, y to \Phi and b to \dot a%

ode1 = diff(w) + diff(y) == -k*x;
ode2 = diff(x) == (k*w)/3 - (k*y)/3;
ode3 = diff(v) + 3*diff(y) == i*k*u;
ode4 = diff(u) == i*k*y - (b*u)/a;
ode5 = (3*b*(diff(y) + (b*y)/a))/a == 4*G*a^2*d*pi*v - k^2*y + 16*G*a^2*d*pi*w;
odes = [ode1; ode2; ode3; ode4; ode5]
[uSol(t), vSol(t), wSol(t), xSol(t), ySol(t)] = dsolve(odes) %Code works, yielding quite "ugly" answers. Next we introduce ICs%

cond1 = x(0) - i*(u(0))/3 == 0;
cond2 = v(0) - 3*w(0) == 0;
cond3 = y(0) - 2*w(0) == 0;
conds = [cond1; cond2; cond3];
[uSol(t), vSol(t), wSol(t), xSol(t), ySol(t)] = dsolve(odes,conds) %Code breaks down, giving the output "Invalid initial conditions"%

 

[phyzguy]

Hmm, I'm not sure, but I do notice two things:
(1) I think your ode3 should be diff(v) + 3*diff(y) == - i*k*u;, no? You have the sign wrong.
(2) You have used the symbol d for both \rho_{DM} and \rho in the last equation. Is that your untent?

I think the code is telling you that you initial conditions are inconsistent. What if you try taking the "ugly" solution you got without the initial conditions and apply the initial conditions one at a time?

 

[JD_PM]

Thanks @phyzguy for the help, I am going to look for more material to read, understand the problem further and then come back.

 

[Geigercounter]

I'm stuggling with a similar problem! Any updates on this thread @JD_PM? or @phyzguy? I've also posted my version of this question on ths forum.

I already found that the above method won't work, because this supposes an analytical solution can be found in Matlab. We'll need to implement a numerical solution, and we'll have to use the ode45 function or similar in Matlab.