Discussion Overview
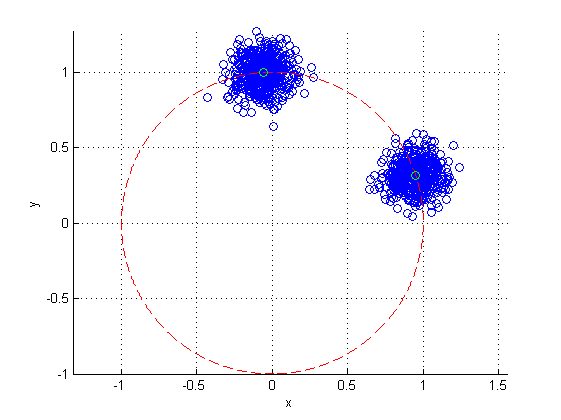
The discussion revolves around estimating two distinct points on the unit circle from noisy x-y coordinate data that contains two clusters. Participants explore various methods for estimation, considering computational limitations and the nature of the noise in the data.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant suggests finding the average of the data points while assuming Gaussian noise, questioning whether the circle is centered at (0,0).
- Another participant proposes calculating the mean of the points and normalizing it to find the closest point on the unit circle, mentioning the need for computational simplicity.
- A different approach involves using a least squares fit with a projection matrix to conform to the equation of a circle, detailing the mathematical formulation required.
- Participants discuss the challenge of separating the clusters, with one suggesting that clustering algorithms could be used, while another expresses reluctance towards iterative methods like k-means.
- There is a suggestion to compute angles of the data points to convert the problem into a 1D clustering task, which may simplify the analysis.
- Concerns are raised about the potential overlap of clusters and the difficulty in ensuring they are well-separated, which complicates the estimation process.
- One participant mentions the idea of binning angles and fitting two Gaussian distributions to identify clusters, indicating an ongoing exploration of this method.
Areas of Agreement / Disagreement
Participants express a variety of approaches and concerns regarding the estimation process, indicating that there is no consensus on a single method. Multiple competing views remain on how best to separate the clusters and estimate the points on the unit circle.
Contextual Notes
Participants note limitations related to computational power and the need for non-iterative methods. The discussion also highlights the uncertainty regarding the separation of clusters and the potential for overlap, which complicates the estimation of the points.