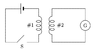
hidemi said:
A. the power supplied to coil 1 is equal to the power delivered by coil 2
B. the emf around coil 1 will be 1/4 the emf around coil 2
C. the current in coil 1 will be 1/4 the current in coil 2
D. the emfs will be the same in the two coils
E. none of the above
.
ans: E
.
In this case, we do not know any information about the current, right?
Therefore, there is no matching answer.
Well, no one else has answered, so I’ll have a go. I think I see what’s going on, but will be happy to be corrected. Sorry if what follows is a bit long-winded.
Is that the complete, exact wording of the question? A few assumptions (which should have been explicitly stated in the question) are probably needed:
- the question refers to the time after the switch is closed;
- the cell and coil-windings are ideal (zero resistance);
- the galvanometer has some non-zero resistance (so the secondary circuit is not a short-circuit).
In addition, the question refers to “the emf around coil 1”. This is confusing – does it mean the cell’s emf, or the back-emf generated in coil 1 when a current flows through it, or something else?
You said: “… we do not know any information about the current, right? Therefore, there is no matching answer.“
That’s not really correct. We can infer certain things about the relationship between primary and secondary currents. And if we don’t even consider currents, we can still use conservation of energy and knowledge of flux in transformers to help us.
You might want to consider these 2 points/questions first:
Q1. Passing a current through a coil (inductance L) sets up a magnetic field which stores energy. If a resistor (R) is then connected across the coil, current flows and decays with time-constant L/R. (in a similar way that a charged capacitor discharges through a resistor). Is that relevant here?
Q2. Are the time-constants for the primary and secondary circuits equal? If not, will this have any signficant effects?
Then consider each answer-option; here are some hints:
A: This option refers to ‘power’, not energy. Is this significant?
B: EDIT: B is a confusing option - are the emfs referred to covering the same time period? This is highly ambiguous.
C: Is the answer to this option related to the answer to option A?
D. Is the answer to this option related to the answer to option B?
You can post your answers to Q1, Q2 and your analysis of A, B, C and D if you want them checked.
If you can sort your way through that lot, you will find option E appears to be correct!