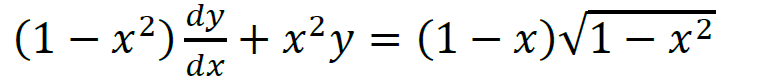SUMMARY
The discussion focuses on solving a linear differential equation by transforming it into the standard form dy/dx + p(x)y = q(x). The equation is manipulated by dividing by (1-x^2), leading to the expression for q(x) as √((1-x)/(1+x)). The integrating factor is derived as μ(x) = exp(∫(x^2/(1-x^2))dx), which is crucial for solving the equation. Participants are encouraged to compute the integrating factor to proceed with the solution.
PREREQUISITES
- Understanding of linear differential equations
- Familiarity with integrating factors
- Knowledge of calculus, specifically integration techniques
- Ability to manipulate algebraic expressions involving square roots
NEXT STEPS
- Compute the integral ∫(x^2/(1-x^2))dx to find the integrating factor μ(x)
- Explore methods for solving linear differential equations using integrating factors
- Study the implications of the solution on the behavior of the original differential equation
- Learn about variations of parameters for non-homogeneous linear differential equations
USEFUL FOR
Students and professionals in mathematics, particularly those studying differential equations, as well as educators looking for practical examples of solving linear differential equations.