Interdependent Recursive Equations

[Himmel]

Hi, I have a system that I am trying so solve in terms of m, and have two recursive equations:

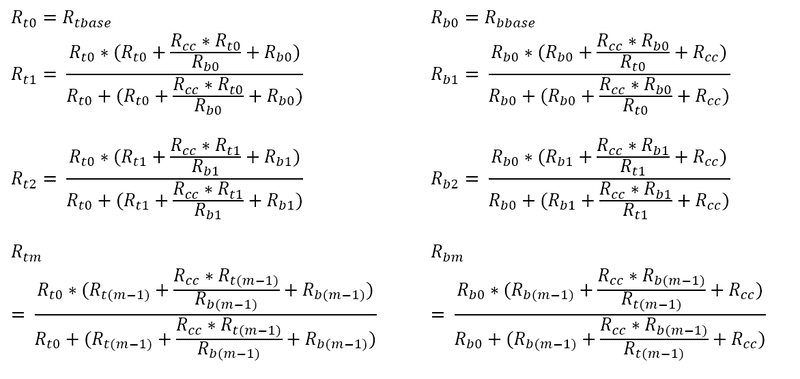
The problem for me is that each recursion is dependent on the value from the other! I know that they are both solvable, however I have no idea what approach I could take to express each only in terms of m. Rbbase, Rtbase and Rcc are all constants, and if it helps Rbbase is proportional to Rtbase.

Cheers, Himmel

 

[andrewkirk]

With sequences like this, where there is obvious way in at first, a good way to develop intuitions that may point towards solutions is to first make numerical calculations of the sequence for a fair number of elements, say twenty. Assume values for the three constants and then use a calculator like R, Python or Matlab to calculate the first twenty values of the two sequences. Then change the constants a few times and see what changes. Hopefully a pattern will start to emerge, suggesting formulas that give values of the sequences in terms of only m and the three constants. For any candidate formula you think of, project the first twenty items using that, and see if they match. If they do, you might then set out to prove that the formula is correct for all m. Induction may well be a handy way to do such a proof.

I also notice that both recursion formulas simplify significantly if you divide both numerator and denominator by the numerator, giving you expressions of the form $\frac{1}{1/R_{bbase}+1/\textrm{messy factor 1}}$ and $\frac{1}{1/R_{tbase}+1/\textrm{messy factor 2}}$ where the 'messy factors' are the second factors in the numerators.

 

[mfb]

Let $K_m = \frac{R_{bm}}{R_{tm}}$. Let $R_{cc}=C$ to avoid overusing R. Let $D=R_{b0}$ so R_b is gone and drop the index "t" on the remaining $R_{tx}$.

Then $$R_{m} = \frac{
R_{0} \cdot \left( R_{m-1}(K_{m-1}+1) + \frac{C}{K_{m-1}} \right)
}{
R_{0} + \left( R_{m-1}(K_{m-1}+1) + \frac{C}{K_{m-1}} \right)
}$$
and
$$K_m R_{m} = \frac{
D \cdot \left( R_{m-1}K_{m-1} + CK_{m-1} \right)
}{
D + \left( R_{m-1}K_{m-1} + CK_{m-1} \right)
}$$
Define $S_m = \frac{1}{R_m}$. And look at m+1 because it shortens the equation. Now
$$S_{m+1} = S_0 + \frac{1}{ \frac{1+K_m}{S_m}+\frac{C}{K_m} }$$
and
$$\frac{S_{m+1}}{K_{m+1}} = \frac{1}{D} + \frac{1}{\frac{K_m}{S_m} + C K_m}$$
I'm still not sure how to find direct expressions, but it looks much nicer already.