Interfacial PDs vs Electrode Potentials

[etotheipi]

Consider the cell $Pt | H_2 | H^+ || Ag^+ | Ag$. I’ve sketched the electric potential against distance across the cell:

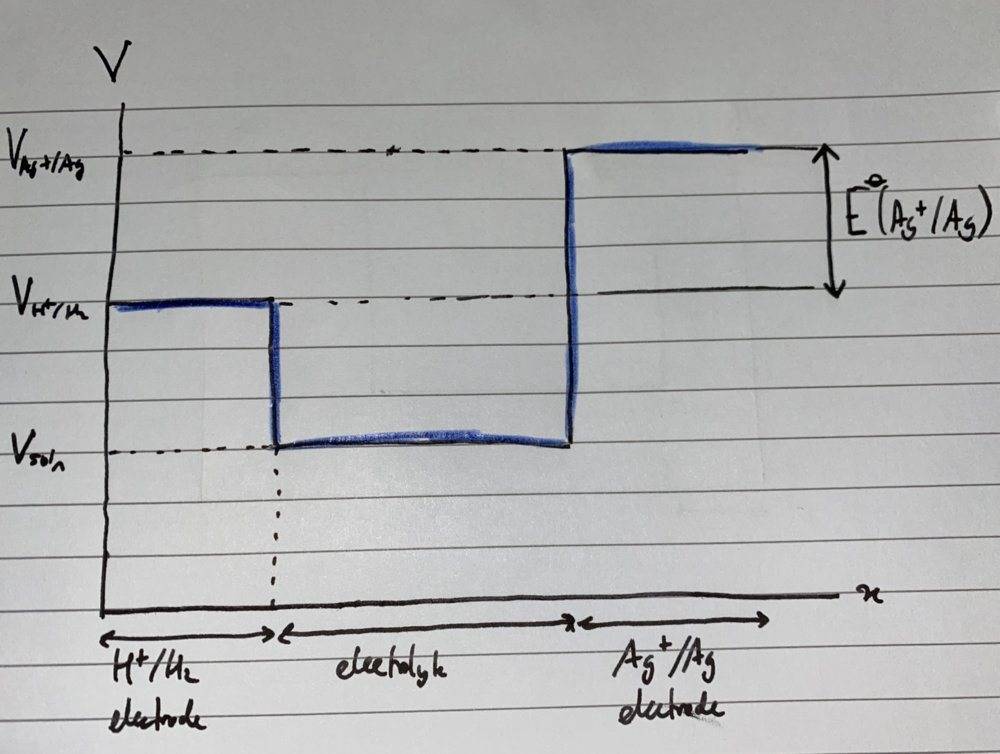
I would think the electrode potential of the $Ag+/Ag$ electrode is $V_{Ag+/Ag} - V_{H^+/H_2}$, which I’ve labelled on the right. We set $V_{H^+/H_2} = 0$ as per convention.

However, my teacher states that the electrode potential equals the interfacial potential difference between the electrode and electrolyte, subtract (relative to) the interfacial potential difference of the reference electrode/electrolyte. This might well be true in this first example, but I don’t think it generalises so can’t be right!

For instance, consider now if we have a potential drop across the electrolyte (e.g. due to an electrolyte-electrolyte interfacial PD or a voltage drop of some other origin). The new potential diagram becomes,

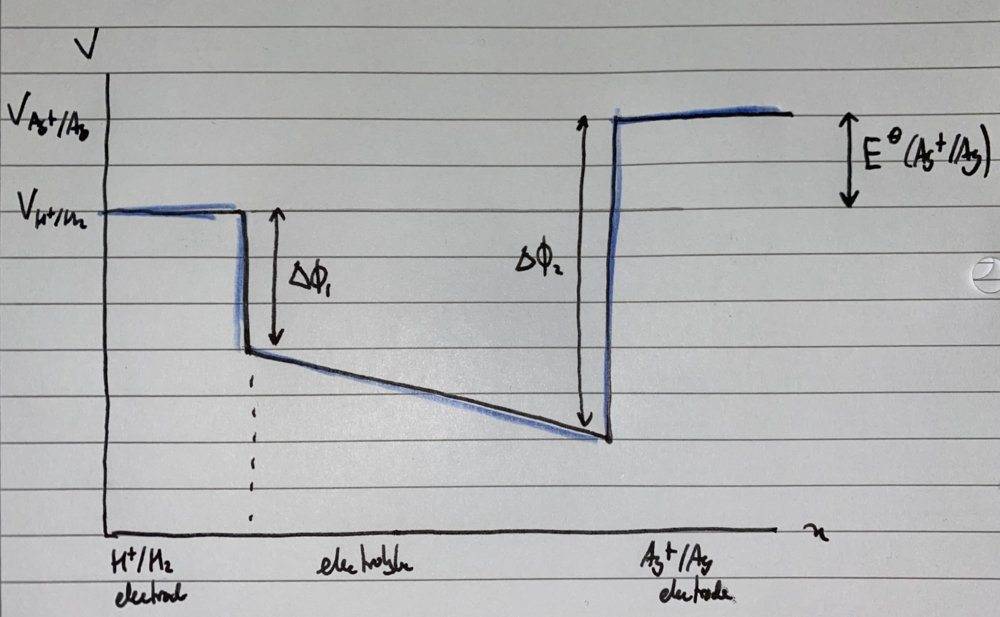
Ostensibly now, my teacher’s definition no longer gives the correct definition of standard electrode potential (the difference of the interfacial potential differences has changed!). Whilst I assume that$V_{Ag+/Ag} - V_{H^+/H_2}$ is still the same as in the first example?

So I wondered whether someone could clarify as to which is correct?

 

[Borek]

If there is no current there is no potential drop "of some other origin" in the electrolyte.

 

[etotheipi]

If there is no current there is no potential drop "of some other origin" in the electrolyte.

Thank you for your reply.

I agree; in that case then I will consider an equilibrium case with a current which approaches zero.

I found a quite illuminating article from the Journal of Chemical Education which says the following, hinging on the IUPAC definition of $E^o$ as the emf of a cell where the couple in question is connected on the right side,

$E_{M^{n+}/M} = (\phi_M - \phi_{M,ref}) = (\phi_M - \phi_{sol}) - (\phi_{M,ref} - \phi_{sol,ref})$

So, it appears my teacher was right! Though this is assuming zero liquid junction potential - I don't know how to correct for this!

In the case of zero liquid junction potential, an electrode potential is then the interfacial potential difference of the electrode in question relative to the interfacial potential difference of the reference electrode - which is arbitrarily set to zero.

Thats sort of weird, because I had assumed we were setting the electrostatic potential of the hydrogen electrode to zero volts, however it appears we are instead defining an (evidently non-zero) potential difference to be zero.

That's quite hard to understand. Are we essentially setting $\phi_{M,ref} = \phi_{sol,ref}$, when in reality they are different (but unmeasurably so!)?