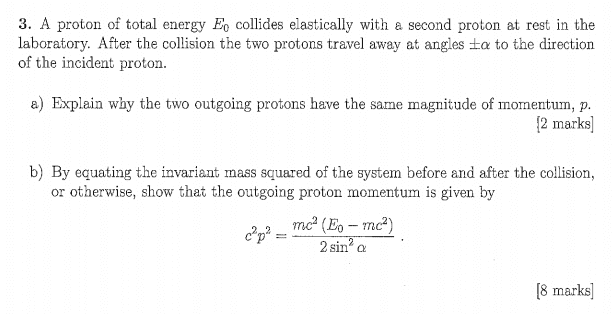SUMMARY
The discussion revolves around solving the invariant mass problem in elastic collisions, specifically focusing on the equations E² = c²p² + m²c⁴ and conservation principles. Participants emphasize the importance of using conservation of momentum and energy, with particular attention to the total energy of protons before and after the collision. The conversation highlights the complexity of algebraic manipulation required to derive the correct expressions without introducing gamma factors, ultimately leading to a derived expression for momentum in terms of energy and angle.
PREREQUISITES
- Understanding of relativistic energy equations, specifically E² = c²p² + m²c⁴
- Knowledge of conservation laws, particularly conservation of momentum and energy
- Familiarity with algebraic manipulation in physics problems
- Basic understanding of elastic collisions in particle physics
NEXT STEPS
- Study the application of conservation of momentum in elastic collisions
- Learn about relativistic energy transformations and their implications
- Explore advanced algebra techniques for solving physics equations
- Investigate the role of gamma factors in relativistic collisions
USEFUL FOR
Physics students, educators, and researchers focusing on particle collisions, relativistic mechanics, and energy conservation principles in high-energy physics.