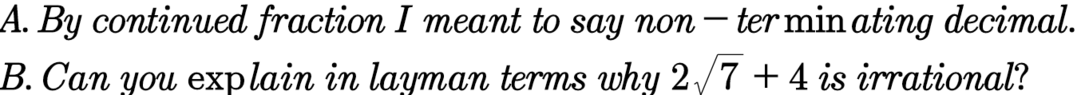- #1
Is 2√(7)+4 an Irrational Number?
- Context: MHB
- Thread starter nycfunction
- Start date
-
- Tags
- Rational
Click For Summary
SUMMARY
The expression \(2\sqrt{7}+4\) is definitively classified as an irrational number. The reasoning hinges on the properties of rational numbers being closed under subtraction and division. If \(x = 2\sqrt{7}+4\) were rational, then \(\sqrt{7}\) would also be rational, leading to a contradiction based on the prime factorization of integers. This contradiction arises from the assumption that integers \(a\) and \(b\) can represent \(\sqrt{7}\) without common factors, which is impossible.
PREREQUISITES- Understanding of rational and irrational numbers
- Basic knowledge of algebraic manipulation
- Familiarity with prime factorization
- Concept of closure properties in mathematics
- Study the properties of irrational numbers in depth
- Learn about the proof techniques for irrationality, such as proof by contradiction
- Explore the concept of closure in mathematical operations
- Investigate other examples of irrational numbers and their proofs
Students of mathematics, educators teaching number theory, and anyone interested in understanding the nature of irrational numbers.
- #2
HallsofIvy
Science Advisor
Homework Helper
- 42,895
- 983
What, exactly, do you mean by "continued decimal number"? If you mean simply that it is not a terminating decimal, a rational number such as 1/3 has that property. That's not the reason $2\sqrt{7}+ 4$ is irrational.
First, the rational numbers are "closed under subtraction and division" so if $x= 2\sqrt{7}+ 4$ were rational so would be $\sqrt{7}= (x- 4)/2$. And if $\sqrt{7}$ were rational then there would exist integers, a and b, with no common factors, such that $\sqrt{7}= \frac{a}{b}$. From that $7= \frac{a^2}{b^2}$ and $a^2= 7b^2$. That is, $a^2$ has a factor of 7 and, since 7 is a prime number, a has a factor of 7. a= 7n for some integer n so $a^2= 49n^2= 7b^2$. Then $b^2= 7n^2$ so, as before, b has a factor of 7, contradicting the fact that a and b has no factors in common.
First, the rational numbers are "closed under subtraction and division" so if $x= 2\sqrt{7}+ 4$ were rational so would be $\sqrt{7}= (x- 4)/2$. And if $\sqrt{7}$ were rational then there would exist integers, a and b, with no common factors, such that $\sqrt{7}= \frac{a}{b}$. From that $7= \frac{a^2}{b^2}$ and $a^2= 7b^2$. That is, $a^2$ has a factor of 7 and, since 7 is a prime number, a has a factor of 7. a= 7n for some integer n so $a^2= 49n^2= 7b^2$. Then $b^2= 7n^2$ so, as before, b has a factor of 7, contradicting the fact that a and b has no factors in common.
Last edited by a moderator:
- #3
Similar threads
- · Replies 5 ·
- · Replies 19 ·
Undergrad
Rational powers of irrational numbers
- · Replies 27 ·
- · Replies 16 ·
- · Replies 7 ·
- · Replies 2 ·
- · Replies 7 ·
- · Replies 10 ·
- · Replies 9 ·