Is my proof of Simon's line theorem complete?

[disregardthat]

I have written a proof of the simons line theorem. I would appreciate if someone would tell me if it's complete.

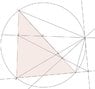
We have $$\Delta ABC$$ inscrubed in a circle, and $$P$$ is an arbitrary point that does not coincide with either of the corners of the triangle. (See attached figure).

Now draw perpendiculars from $$P$$ to $$[AB]$$, $$[AC]$$ and $$[BC]$$ which intersect with the lines in $$U, \ Y$$ and $$Z$$ respectively.

Let $$E$$ be the point of intersection between $$[PU]$$ and $$[AY]$$.
Let $$T$$ be the point of intersection between $$[AC]$$ and $$[BP]$$.

Let $$\angle BZP=\alpha$$ and $$\angle APU=\beta$$.

Now as $$\angle BZP$$ and $$\angle BUP$$ are supplementary, $$BZPU$$ is a cyclic quadrilateral $$\Rightarrow \angle PUZ = \alpha$$.

Now as $$\angle PAC$$ subtend over the same arc as $$\angle PBZ, \ \angle PAC = \alpha \Rightarrow \angle UAR = 90 - (\alpha +\beta) \Rightarrow \angle ARU = \alpha + \beta \Rightarrow \angle PET = \alpha +\beta$$.

Let $$\angle UZB = \gamma \Rightarrow \angle UPB = \gamma$$.

As $$\angle CYP$$ and $$\angle CZP$$ are supplementary, $$CZPY$$ is a cyclic quadrilateral $$\Rightarrow \angle CPY = \gamma$$.

As $$\angle PAY =\angle PUY$$, $$APYU$$ is a cyclic quadrilateral $$\Rightarrow \angle UYA = \beta$$.

Now $$\angle ETP =180-(\alpha +\beta + \gamma) \Rightarrow \angle PTY = \alpha +\beta +\gamma \Rightarrow \angle TPY=90-(\alpha+\beta+\gamma)$$

Now as $$\angle BUZ=\angle BPZ$$ and $$\angle BUZ=90 - \alpha, \angle BPZ = 90 - \alpha$$.
Let $$\angle CPZ= \mu$$. Now $$\angle CPZ+\angle TPC=\angle BUZ \Rightarrow \mu + 90-(\alpha +\beta)=90-\alpha \Rightarrow \mu = \beta \Rightarrow \angle CPZ = \beta \Rightarrow CYZ = \beta$$.

As $$\angle UYP+\angle PYZ = \beta +90 + 90-\beta = 180, U, \ Y$$ and $$Z$$ must be colinear.

$$QED$$

Thanks for any feedback.

 

[disregardthat]

Just bumping this... Hoping someone will take a look. I really appreciate it.

 

[rocomath]

Where is $$\angle APX$$ or rather point X.

 

[disregardthat]

I thought I had switched all the X's with U's as my program wouldn't accept X as a vertex. It's really U. It's changed now.

 

[rocomath]

What program are you using?

 

[disregardthat]

Geogebra. It's great. It's free and our textbooks webpage has a link to it.

If you want it..: here is a direct link to the setup file.
http://www.geogebra.org/download/InstData/Windows/NoVM/GeoGebra_3_0_0_0_Release_Candidate_1.exe

 

[rocomath]

Woah! This program is cool ... thanks! I wish I knew more geometry to help you, lol. I'm actually self-studying it at the moment, but you're further ahead of me in the game so :( I'm sure someone else will respond in a few!

 

[disregardthat]

It's supposed to be Simson's line, and not Simons line.

 

[naveeniitkgp]

PZ is perpendicular to BC, then angle(BZP) is naturally 90 degree, no need for any assumption!