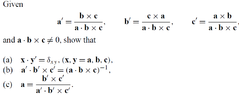Is There a Better Way to Approach Vector Identities?

[ognik]

Please excuse my copying this question in, minimising my input :-)
View attachment 4920

Part (b): Let $ a.b \times c =v $
Then $ a'.b' \times c' = \left( \frac{b \times c}{v}\right) . \left( \frac{c \times a}{v} \times \frac{a \times b}{v}\right) $

$ = v^{-1} \left(b \times c\right). \left[ \left(c \times a\right) \times \left(a \times b\right) \right] $

From a previous exercise, $ \left(a \times b\right) \times \left(c \times d\right) = \left(a.b \times d\right)c - \left(a.b \times c\right)d $ ...

I get $ v^{-1} \left(b \times c\right). \left[ \left(c.a \times b\right)a - \left(c.a \times a\right)b \right] $
the $a \times a$ term = 0, but I am not sure of the laws around something like $ \left(c.a \times b\right)a $

I don't think I can do $ \left(c.a.a \times b.a\right) $ ? So I'm a bit stuck here, maybe there's a better way to approach this..

 

[Ackbach]

With your definition of $v=\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c})$, we have
\begin{align*}
\mathbf{a}'\cdot(\mathbf{b}'\times\mathbf{c}')&=\frac{1}{v^3}\left[(\mathbf{b}\times\mathbf{c})\cdot
((\mathbf{c}\times\mathbf{a})\times(\mathbf{a}\times\mathbf{b}))\right] \\
&=\frac{1}{v^3}\left[(\mathbf{b}\times\mathbf{c})\cdot
[(\mathbf{c}\cdot(\mathbf{a}\times\mathbf{b}))\mathbf{a}-\underbrace{(\mathbf{c}\cdot(\mathbf{a}\times\mathbf{a}))\mathbf{b}}_{=\mathbf{0}}]\right] \\
&=\frac{\mathbf{c}\cdot(\mathbf{b}\times\mathbf{a})}{v^3} \, [(\mathbf{b}\times\mathbf{c})\cdot\mathbf{a}].
\end{align*}
Recognizing that $\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c})=\mathbf{b}\cdot(\mathbf{c}\times\mathbf{a})
=\mathbf{c}\cdot(\mathbf{a}\times\mathbf{b})$, can you finish?

 

[ognik]

$\frac{\mathbf{c}\cdot(\mathbf{b}\times\mathbf{a})}{v^3} \, [(\mathbf{b}\times\mathbf{c})\cdot\mathbf{a}].$

Its this step I am struggling with, can't see what (identity?) gets this from the previous step?

 

[Ackbach]

There's a property of the dot product. Suppose $\mathbf{a}$ and $\mathbf{b}$ are vectors, and $c$ is a scalar. Then it is a fact that $\mathbf{a}\cdot(c\mathbf{b})=c(\mathbf{a}\cdot\mathbf{b})$. Then, it's very important to remember that the result of a cross product is a vector, and the result of a dot product is a scalar. It follows that
\begin{align*}
\mathbf{a}'\cdot\left(\mathbf{b}'\times\mathbf{c}'\right)&=\frac{1}{v^3}\left[(\mathbf{b}\times\mathbf{c})\cdot
((\mathbf{c}\times\mathbf{a})\times(\mathbf{a}\times\mathbf{b}))\right] \\
&=\frac{1}{v^3}\left[\underbrace{(\mathbf{b}\times\mathbf{c})}_{\text{vector}}\cdot
[\underbrace{(\mathbf{c}\cdot(\mathbf{a}\times\mathbf{b}))}_{\text{scalar}} \; \mathbf{a}-\underbrace{(\mathbf{c}\cdot(\mathbf{a}\times\mathbf{a}))\mathbf{b}}_{=\mathbf{0}}]\right] \\
&=\frac{1}{v^3}\left[\underbrace{(\mathbf{b}\times\mathbf{c})}_{\text{vector}}\cdot
[\underbrace{(\mathbf{c}\cdot(\mathbf{a}\times\mathbf{b}))}_{\text{scalar}} \; \mathbf{a}\right] \\
&=\frac{\mathbf{c}\cdot(\mathbf{b}\times\mathbf{a})}{v^3} \, [(\mathbf{b}\times\mathbf{c})\cdot\mathbf{a}].
\end{align*}
Does that answer your question?

[EDIT] See below for a correction.

 

[ognik]

It did finally, and just checking - in the c.(A x B) did you accidentally swap A x B to B x A ?

 

[Ackbach]

It did finally, and just checking - in the c.(A x B) did you accidentally swap A x B to B x A ?

You're quite right. It should be $\mathbf{c}\cdot(\mathbf{a}\times\mathbf{b})$ in the last line. Good catch, and thank you!

 

[ognik]

It feels good to be getting better - and a significant amount of thanks is due to yourself and others who have helped me this year! While I am happy working on my own, I do miss the interaction of a University environment, it makes more of a difference than I expected.