Jurgen M
Has any path/line/shape/contour function? And how find function of complex "path"?
for example this?
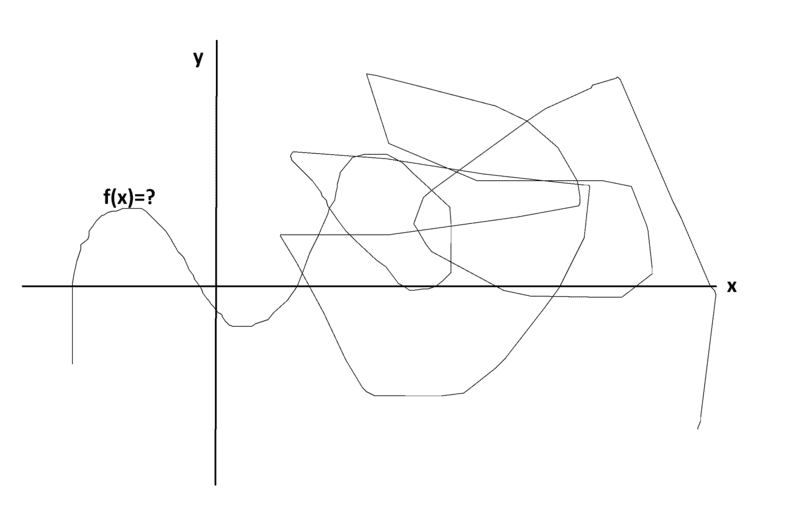
for example this?
The discussion revolves around whether every possible path, line, shape, or contour can be represented by a function. Participants explore the implications of paths that backtrack on themselves and the concept of parameterization in relation to functions.
Participants express multiple competing views on the representation of paths as functions, with no consensus reached on whether every path can be represented or how to approach the problem of backtracking paths.
Limitations include the ambiguity in defining what constitutes a path versus a function, and the unresolved nature of how to accurately represent complex paths mathematically.
No.Why?jedishrfu said:Well since your function backtracks on itself then no there is no equation f(x) that can represent it.
Do you know why?
However, if you parametrize both x and y with some variable called t then maybe you can piece together a vector function to imitate the path above.
You have to distinguish between the path, and the relation ##\{(x,f(x))\}##. What do you want to talk about? One is a function ##\mathbb{R} \longrightarrow \mathbb{R}^2## and the other a subset of ##\mathbb{R}^2##.Jurgen M said:What is procedure to find f(x) of some given complex path that is not backtracks itslef?
It can not be in the form of f(x) because, for a single value of x, there are multiple values of y that are matched with it on the path. Which y-value should f(x) be?Jurgen M said:No.Why?
What is procedure to find f(x) of some given complex path that is not backtracks itslef?
Slowly.fresh_42 said:You have to distinguish between the path, and the relation ##\{(x,f(x))\}##. What do you want to talk about? One is a function ##\mathbb{R} \longrightarrow \mathbb{R}^2## and the other a subset of ##\mathbb{R}^2##.
As long as this isn't answered, this thread will be a mess.
I answered this in post #4. A path is a walkthrough of the line you drew (every point has a unique timestamp), from a starting point to an endpoint. If you consider ##f(x)## as a function graph, then it is a) not a function because there are points ##x## with two different values ##f(x)##, and b) a subset of the plane. Such a subset can be considered as a relation. Relations allow ambiguities, functions do not.Jurgen M said:Slowly.
First I don't understand this math terms..
What is difference between "path" and f(x)?
That's a guess. Therefore post #6. As long as everybody chooses for himself what the OP might have meant, as long will this thread be doomed to confusion.mcastillo356 said:It's a relation, as far as I know (I am speaking without background; but I find interesting this thread) You are never express algebraically that path without a huge effort.
You might be surprised at how well Fourier series can approximate such things. See this (especially the first few minutes).mcastillo356 said:It's a relation, as far as I know (I am speaking without background; but I find interesting this thread) You are never express algebraically that path without a huge effort.
We distinguish between a "formula" and a "function".mcastillo356 said:It's a relation, as far as I know (I am speaking without background; but I find interesting this thread) You are never express algebraically that path without a huge effort.
If only a picture is given, then we can get arbitrary close with formulas and piecewise-defined paths.jbriggs444 said:The answer to that question is no. Unless I am misremembering, the cardinality of the set of continuous ideal paths is the cardinality of the continuum and the cardinality of the set of formulas is aleph null.
Yes, and ##G:=\{(x,y)\in \mathbb{R}^2\,|\,y=f(x)\}\subseteq \mathbb{R}^2## is a relation, and in the case of ##f## as in post #1 not a function.FactChecker said:Just to be clear, when a path is parameterized by a variable ##t \in [0,1]##, like ##P: f(t) = ( x(t), y(t) ), t \in [0,1]##, that is a function from ##[0,1]## to ##\mathbb{R}^2##.
It is something akin to cheating, but even if the path cannot be parameterized as a continuous function over the reals, one can nonetheless unambiguously associate a real number t with each (x,y) coordinate in the graph (e.g. by interleaving the digits in the decimal expansions) and then declare f(t) = (x,y) and set the domain to the set of t values that are used. It is unlikely that this function will be continuous, but it will be a function from [a subset of] ##\ \mathbb{R}\ ## to the set of coordinates of points with pencil marks.WWGD said:I think this question is equivalent to whether every path can be parameterized. It seems that if it's rectifiable, it may be parameterized by arc length.
How about just using the ortho projections to the respective axes as the coordinates. Wonder if this is specific enough for the op?jbriggs444 said:It is something akin to cheating, but even if the path cannot be parameterized as a continuous function over the reals, one can nonetheless unambiguously associate a real number t with each (x,y) coordinate in the graph (e.g. by interleaving the digits in the decimal expansions) and then declare f(t) = (x,y) and set the domain to the set of t values that are used. It is unlikely that this function will be continuous, but it will be a function from [a subset of] ##\ \mathbb{R}\ ## to the set of coordinates of points with pencil marks.