Is this a complex number at the second quadrant?

[mcastillo356]

TL;DR

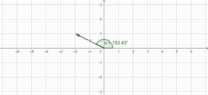
I am quite sure, but I don't manage with Geogebra. It involves the value of the $\arg(w)$ in the interval $-\pi<\theta\leq{\pi}$, called the principal argument of $w$ and denote it $\mbox{Arg(w)}$

Hi, PF, so long, I have a naive question: is $\pi+\arctan{(2)}$ a complex number at the second quadrant? To define a single-valued function, the principal argument of $w$ (denoted $\mbox{Arg (w)}$ is unique. This is because it is sometimes convenient to restric $\theta=\arg{(w)}$ to an interval of length $2\pi$, say the interval $0\leq{\theta}<2\pi$, or $-\pi<\theta\leq{\pi}$. This last one is which I am concerned with.
PS: I post without preview
Regards!

 

[pbuk]

Hi, PF, so long, I have a naive question: is $\pi+\arctan{(2)}$ a complex number at the second quadrant?

No, it is a real number about equal to 4.25.

 

[mcastillo356]

Hi, PF

If $a<0$ and $b>0$, are we at the second quadrant, therefore $\arg{(a+bi)}=\pi+\arctan{(b/a)}$?.
If so, $\pi+\arctan{(2)}$ should fall at the second one. I'm quite sure of it. But then, which is the complex number that has $\pi+\arctan{(2)}$ as the principal value of the argument?

My attempt: $w=-2+i$. But here comes the problem: $\displaystyle\frac{1}{-2}\neq{2}$, so the statement $\arg{(a+bi)}=\pi+\arctan{(b/a)}$ must be false. The question is that is a true statement. The solution is, in my personal opinion, that the moduli $|-2+i|=\sqrt{5}$, and the $\mbox{Arg}$ ought to be, $\pi+\arctan{-2}$.

Regards!

 

[pbuk]

If $a<0$ and $b>0$, are we at the second quadrant, therefore $\arg{(a+bi)}=\pi+\arctan{(b/a)}$?

Yes.

If so, $\pi+\arctan{(2)}$ should fall at the second one. I'm quite sure of it.

No. If $a<0$ and $b>0$ then $\frac b a \ne 2$.

But then, which is the complex number that has $\pi+\arctan{(2)}$ as the principal value of the argument?

As already discussed $\pi+\arctan{(2)} \approx 4.25$. Is this between $-\pi \text{ and } \pi$?

My attempt: $w=-2+i$. But here comes the problem: $\displaystyle\frac{1}{-2}\neq{2}$, so the statement $\arg{(a+bi)}=\pi+\arctan{(b/a)}$ must be false. The question is that is a true statement. The solution is, in my personal opinion, that the moduli $|-2+i|=\sqrt{5}$, and the $\mbox{Arg}$ ought to be, $\pi+\arctan{-2}$.

I don't really understand any of that, but $\arg(-2 + i) = \pi - \arctan \frac 1 2$.

 

[mcastillo356]

No. If $a<0$ and $b>0$ then $\frac b a \ne 2$.

Oops!

As already discussed $\pi+\arctan{(2)} \approx 4.25$. Is this between $-\pi \text{ and } \pi$?

Not at all

I don't really understand any of that, but $\arg(-2 + i) = \pi - \arctan \frac 1 2$.

Need to revisit my background in complex numbers. Thanks for your attention, hope we will keep in touch. Regards!

 

[mcastillo356]

I don't really understand any of that, but $\arg(-2 + i) = \pi - \arctan \frac 1 2$.

Understood. Let's see if my drawing agrees with your quote. $\pi-\arctan\frac 1 2$, could be $\mbox{Arg}$ of $w=(-2+i)$, $\pi$ counterclockwise, and $\arctan \frac 1 2$ clockwise?

I don`t manage with $\pi+\arctan(-2)$. I've tried with a Casio fx-82MS, pretending to switch polar to rectangular coordinates: I won't bore the forums with my effort; I just declare that my attempt is $\pi+\arctan(-2)=-0.1\mbox{radians}$.
I post with no preview
Regards!
PS: Edited. Reason: Mistake when describing the Geogebra file.

 

[mcastillo356]

I don't really understand any of that,

Neither me; how many days have I taken?

but $\arg(-2 + i) = \pi - \arctan \frac 1 2$.

Thank you very much!
Greetings.

 

[mcastillo356]

Hi, PF, write to say how misled was I when saying that the $\mbox{Arg}$ corresponding to $w=(-2 +i)$ was $\pi + \arctan(-2)=-60.29\;\mbox{degrees}$. Actually placing $w$ at the fourth quadrant