- #1
momentum
- 111
- 0
Hi,
I was trying to draw a plan 2,0,0 in X,Y,Z co-ordinate system
Is it correctly drawn ?
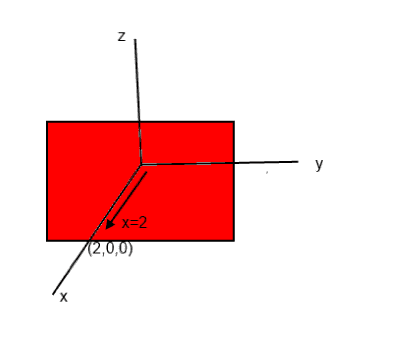
I think ...I'm wrong in drawing this plane
I think I'm wrong because each point in this plane has non zero y & z value...they are not having y=0& z=0 everywhere all the time although x=2 everywhere on this plane...so my drawing to plane (2,0,0) is wrong.
Could you please correct my analysis ?
If I'm wrong then what is correct way to draw the plane (2,0,0) ?
I was trying to draw a plan 2,0,0 in X,Y,Z co-ordinate system
Is it correctly drawn ?
I think ...I'm wrong in drawing this plane
I think I'm wrong because each point in this plane has non zero y & z value...they are not having y=0& z=0 everywhere all the time although x=2 everywhere on this plane...so my drawing to plane (2,0,0) is wrong.
Could you please correct my analysis ?
If I'm wrong then what is correct way to draw the plane (2,0,0) ?