Issue about the percentage of falling of height of Likelihood

[fab13]

I have currently an issue about the height at which the projection of 1 sigma edges in 2D contour should intersect the associated Likelihood.

Here a figure to illustrate my issue :

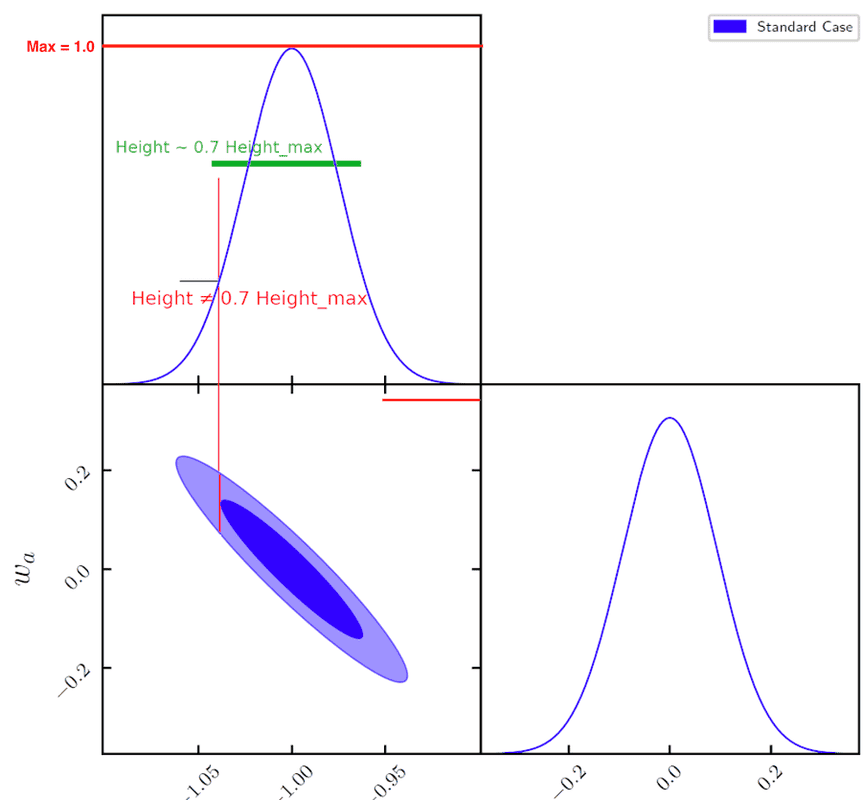At bottom left is represented the joint distribution (shaded blue = contours at 2 sigma (95% C.L) and classic blue = contours at 1 sigma (68% C.L) of the 2 parameters considered (w0 and wa).
On the top is represented the normalized Likelihood of w0 parameter.

In all contours (with all triplot representing other parameters) and in all tripltot of thesis documents I have seen, the projection from the edge of 1 sigma contours on the likelihood intersects the likelihood at a height relatively low (on my scheme, roughly at 25%-30%, at first sight, of the maximum height of the likelihood).

However, one tells me that Likelihood should be intersected by the 1 sigma edge of joint distribution at roughly 70% of the maximum height of Likelihood (green bar and text on my figure)

For this, he justifies like this :

Concerning $$\Delta \chi^{2}$$, distribution function is a `\chi^2` law with 2 freedom degrees ; pdf is written as :

$$ f(\Delta\chi^{2})=\dfrac{1}{2} e^{-\dfrac{\Delta\chi^{2}}{2}} $$

So for a fixed `confidence level C.L`, we have :

$$1-CL= \int_{\Delta\chi^{2}_{CL}}^{+\infty}\dfrac{1}{2}e^{-\dfrac{\Delta\chi^{2}}{2}}\text{d}\chi^{2}$$

`$$=e^{-\dfrac{\Delta\chi_{CL}^{2}}{2}}` $$

and taking `CL=0.68`, we get :

$$ \Delta \chi ^{2}_{CL}=-2\ln(1-CL) $$

$$ \Delta \chi^{2}_{CL}=2.28 $$

And Finally, he concludes by saying that Maximum of Likelihood shoud fall from about 30% , i.e :

$$ e^{-\dfrac{(2.3)^2}{2}} = 0.31 $$

So I don't know why I get a falling of about 70% ~ (1-0.31) and not only of 31% ~ 0.3 like one says on my figure (red line on my figure above).

ps1 : I have seen an ineresting remark on https://docs.scipy.org/doc//numpy-1.10.4/reference/generated/numpy.random.normal.html which suggests a maximum at 60.7% of the max, which is not really what I expect (~ 70%).

ps2 : I have also found another interesting page, maybe more important since it talks about multivariate distribution :

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.multivariate_normal.html

and here too, a justification of my reasoning :

If someone could explain me the trick to get an intersection at 70% of the maximal height of normalized Likelihood ...

Any help is welcome. [1]: https://i.stack.imgur.com/SXB1K.png
[2]: https://i.stack.imgur.com/2O8xi.jpg

 

[pbuk]

Isn't this just the difference between a 1- and 2-tailed test?

 

[mfb]

The 2 degrees of freedom are the key point here. "1 sigma" covers a larger likelihood range. There are two distributions where you can (and expect to) "lose" likelihood relative to the peak. The outer edge might be less likely in one distribution but it's then the peak of the other distribution (conditional if they are correlated).

 

[fab13]

So, it is impossible to justify this "lose" lileklihood of ~ 30% with 1C.L of 2D contours ? if yes, what is expected as percentage of "losing" factor if I take the projection from the 1 C.L of 2D contours on 1D Likelihood ?

Thanks

 

[mfb]

I don't understand what you are asking, but check the chi2 distribution.

 

[fab13]

yes, I did above a small calculus which represents the $\Delta\chi2$ for 2 degrees of freedom when we are at 1 C.L. It gives a $\Delta\chi2 = 2.28$.

Such way that I have a height of $exp(-\Delta\chi2/2) = 0.3198$. It would correspond to a falling of ~ 0.32 from the maximal height, do you agree ?

Otherwise, which value (height) is expected for intersection when I project the 1 C.L 2D contours on the Likelihood (like for example on my figure at the beginning of the post) ?

Best regards

 

[fab13]

Finally, is thre anyone who tells me if, on my initial top figure of the post, the vertical bar represents what is expected, i.e only roughly 30% of the max height of Likelihood ?

Any advise is welcome