MHB Jesus' question at Yahoo Answers regarding finding total cost function

[MarkFL]

Here is the question:

Function Math Question?

I am having a problem solving this question, any help is appreciated!

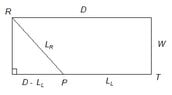
An oil refinery is located on the north bank of a straight river that is 2 km wide. A pipeline is to be constructed from the refinery to a point P on the south bank of the river, and then along the river to storage tanks on the south side of the river 6 km east of the refinery. The cost of laying pipe is $400,000 per km over land, and $800,000 per km under the river. Express the total cost of the pipeline as a function of the distance from P to the storage tanks.

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Jesus,

I would first label some variables:

$$L_R$$ = the length of the pipeline under the river.

$$L_L$$ = the length of the pipeline over land. This is the variable with which we are to express the total cost function.

$$D$$ = the distance downriver the tanks are from the refinery.

$$W$$ = the width of the river.

$$C_R$$ = cost in dollars per unit length to lay pipe under the river.

$$C_L$$ = cost in dollars per unit length to lay pipe over the land.

Next, let's draw a diagram:

View attachment 1022

$R$ is the location of the refinery, and $T$ is the location of the tanks.

We see that by Pythagoras, we have:

$$L_R=\sqrt{\left(D-L_L \right)^2+W^2}$$

Now, the total cost is given by:

$$C=C_RL_R+C_LL_L$$

Substituting for $L_R$, we have:

$$C\left(L_L \right)=C_R\sqrt{\left(D-L_L \right)^2+W^2}+C_LL_L$$

Using the given data for the parameters:

$$C_R=800000,\,D=6,\,W=2,\,C_L=400000$$

we have:

$$C\left(L_L \right)=800000\sqrt{\left(6-L_L \right)^2+2^2}+400000L_L$$

Factoring and simplifying, we have:

$$C\left(L_L \right)=400000\left(2\sqrt{L_L^2-12L_L+40}+L_L \right)$$