Karl Schwarzschild: Solving GR on the Eastern Front

[BWV]

Read the bio / fiction chapter on Karl Schwarzschild in Benjamin Labatut’s great Book, and curious on a little color on how he developed the solution - I had thought finding an exact solution in GR was just math chops, but actually any Lorentzian metric is an exact solution, so the difficulty was in finding a solution that reproduced the physics, but what physics would Swchwarzchild had in 1915 on the Eastern front - just the precession of Mercury, which was in the copy Einsteins GR paper he has?

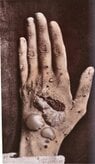
FWIW, he was not directly in the trenches, he foolishly volunteered at age 40 to serve as an artillery specialist where he could employ abilities. He also was wasting away with Pemphigus, a nasty genetic skin disease that Ashkenazi Jews are susceptible to

 

[PeterDonis]

what physics would Swchwarzchild had in 1915 on the Eastern front

He had Einstein's field equation; Einstein had sent him a preprint of his paper giving the final correct version of the field equation. He then looked for a solution that satisfied the assumptions of vacuum (zero stress-energy) and spherical symmetry, and found the solution that now bears his name. We now know that this is the unique solution for those conditions (this result is known as Birkhoff's Theorem and was proved, IIRC, in the early 1920s).

just the precession of Mercury, which was in the copy Einsteins GR paper he has?

Schwarzschild wasn't interested in solving the weak field limit; EInstein had already done that and showed that the precession of Mercury came out. He was interested in the most general possible solution for the conditions given (vacuum and spherical symmetry). (He also found a solution for the case of spherical symmetry and a perfect fluid with constant density, i.e., describing a highly idealized spherical planet or star.)

 

[PeterDonis]

any Lorentzian metric is an exact solution

In the sense that you can compute its Einstein tensor and call that, adjusted by an appropriate constant factor, the "stress-energy tensor" of your solution, yes. But, as you note, this makes no guarantee whatever that the resulting solution will describe anything physically reasonable.

The more usual approach is to make some reasonable assumptions about things like symmetries of the spacetime (as Schwarzschild assumed spherical symmetry) and some general form for the stress-energy tensor (as Schwarzschild assumed vacuum, and then for his other solution he assumed a perfect fluid with constant density). That allows you to simplify the form of the metric using the symmetries, compute its Einstein tensor to give a set of differential equations for the metric components, and then use your assumption about the stress-energy tensor to determine the solution.

 

[BWV]

Karl’s son Martin was an accomplished Astrophysicist, who fortunately fled Germany in the 30s and worked for US intelligence during the war, before landing at Princeton where he worked on stellar evolution, dying in 1997. No doubt some here knew him

 

[vanhees71]

He had Einstein's field equation; Einstein had sent him a preprint of his paper giving the final correct version of the field equation. He then looked for a solution that satisfied the assumptions of vacuum (zero stress-energy) and spherical symmetry, and found the solution that now bears his name. We now know that this is the unique solution for those conditions (this result is known as Birkhoff's Theorem and was proved, IIRC, in the early 1920s).

Amazingly, he also gave a first solution for a "compact star" (non-vacuum solution, using the model of an incompressible fluid). Both papers appeared in the "Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften (Berlin) 1916":

https://ui.adsabs.harvard.edu/abs/1916SPAW...189S/abstract
https://ui.adsabs.harvard.edu/abs/1916skpa.conf..424S/abstract