Kubo Formula Deriviation - interaction picture, complete eigenbasis

[binbagsss]

Hi I'm looking at David Tong notes on QHE http://www.damtp.cam.ac.uk/user/tong/qhe/two.pdf (page 56), I've attached the relevant screenshot below also.

I understand we are working in the interaction picture whereby states evolve via the Unitary Operataor EQ 2.10 in the notes(I think this is possibly called Dyson's formula) and operators evolve via $e^{-iH_o t/\bar{h}}O(t=0)e^{iH_0 t\/\bar{h}}=O(t=t)$ (*), where $H_0$ is the unperturbed Hamiltonian and $O$ an operator.

I follow up until the top of page 56, but am stuck on the next part when we 'insert complete basis of the energy eigenstates of $H_0$

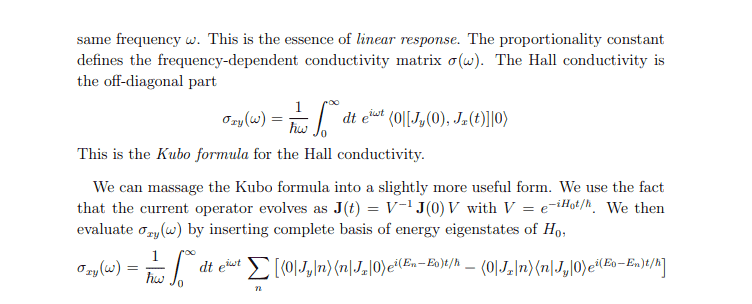First of all, let me check my understanding on the notation and concepts. So we have a system perturbed by $\Delta{H(t)}$ and at the top of page 54, where we say $H_0 |m>=E_m |m> ,m>$ (**)the energy eigentates of $H_0$. Now to check when we speak of the ground-state |0> (obtained by evolving $t \to -\infty$ etc) , would one also refer to this, then, as a eigenstate of $H_0$.

Most importantly, when we use the notation $| n>$ as the complete eigenbasis, we are referring to the perturbed states right? So to get from the expression at the top of page 56 to the next expression, we have already input the time evolution of the state 0>, but not n> (and not the operator )?

But if so, I am totally stuck how we then get the next line, since there seems to be no further use of the unitary operator $U(t)$ but instead two applications of something similar to (*).

However to deal with the $J_x(t)$ wouldn't we get for this term $J_x(t) \to e^{-iH_o t/\bar{h}}J_x(t=0)e^{iH_0 t\bar{h}}$. Now I'm confused also how once translates $H_0$ to a specific energy- $H_0$ tells us the system is in the unperturbed state right? I.E any of one of these eigenstates which satisfy (**)? So where have we picked and chose $E_n$ and $E_0$ from? Have we assumed the system is in the state with energy $E_0$ at $t=0$, and then $E_n$ is the system at time $t$? what has actually allowed us to replace $H_0$ with $E_i$.

Finally, to sound stupid, am i right in thinking we can take these exponentials outside because they have no spatial dependence and the operator $J$ is made up from spatial derivatives only? But if this is the case, say if we have $< n | B | n>$ for $B$ some operator, and $B$ is again only made up of spatial derivative operators, then, apply (*), we would be able to take this out of the bra-ket, and the exponential factors would cancel.

Apologies I'm pretty confused.

 

[king vitamin]

Most importantly, when we use the notation $|n\rangle$ as the complete eigenbasis, we are referring to the perturbed states right?

No, the states $|n\rangle$ are the eigenstates of $H_0$:
$$
H_0 |n\rangle = E_n |n\rangle.
$$

Now I'm confused also how once translates H0H0H_0 to a specific energy- H0H0H_0 tells us the system is in the unperturbed state right? I.E any of one of these eigenstates which satisfy (**)? So where have we picked and chose EnEnE_n and E0E0E_0 from? Have we assumed the system is in the state with energy E0E0E_0 at t=0t=0t=0, and then EnEnE_n is the system at time ttt? what has actually allowed us to replace H0H0H_0 with EiEiE_i.

I think you've confused yourself by trying to think of starting in some initial state and evolving to some final state. All Tong is trying to do is evaluate a ground-state expectation value of a particular time-dependent operator. Then you just turn the crank (I'll take hbar=1):
$$
\langle 0 | J_y e^{i H_0 t} J_x e^{- i H_0 t} - e^{i H_0 t} J_x e^{- i H_0 t} J_y | 0 \rangle = \sum_{n}\left[\langle 0 | J_y | n \rangle \langle n | e^{i H_0 t} J_x e^{- i H_0 t} - e^{i H_0 t} J_x e^{- i H_0 t}| n \rangle \langle n | J_y | 0 \rangle\right].
$$
But then you can just use $H_0 |n\rangle = E_n |n\rangle$ to evaluate the exponentials, and you get
$$
\sum_{n}\left[\langle 0 | J_y | n \rangle \langle n | J_x \rangle0 e^{i (E_n - E_0) t} - \langle 0 |J_x | n \rangle \langle n | J_y | 0 \rangle e^{-i (E_n - E_0) t} \right]
$$