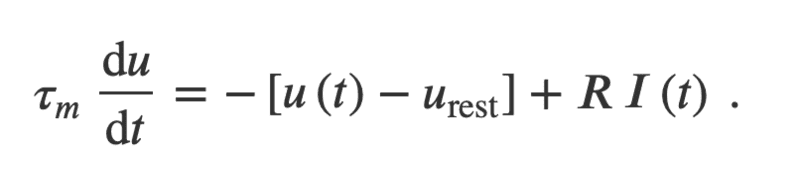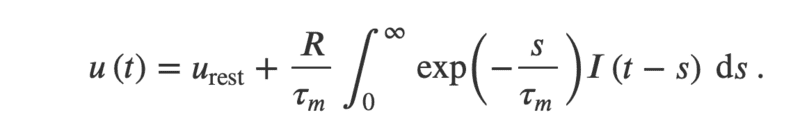SUMMARY
The forum discussion focuses on the solution to the Leaky Integrate-and-Fire (LIF) neuron model's differential equation for arbitrary time-dependent current, as presented in the book "Neural Dynamics." The discussion emphasizes the mathematical steps outlined by the author, which are crucial for understanding the dynamics of neural responses to varying inputs. Key aspects include the formulation of the differential equation and the analytical techniques used to derive the solution, which are essential for modeling neuronal behavior accurately.
PREREQUISITES
- Understanding of differential equations, particularly in the context of neural models.
- Familiarity with the Leaky Integrate-and-Fire (LIF) neuron model.
- Basic knowledge of time-dependent functions and their applications in neuroscience.
- Proficiency in mathematical analysis techniques relevant to neural dynamics.
NEXT STEPS
- Study the mathematical derivation of the LIF neuron model from "Neural Dynamics."
- Explore numerical methods for simulating LIF neuron responses to arbitrary current inputs.
- Investigate the implications of time-dependent current on neuronal firing patterns.
- Learn about alternative neuron models and their comparative dynamics with LIF neurons.
USEFUL FOR
Neuroscientists, computational neuroscientists, and researchers interested in modeling neuronal dynamics and understanding the effects of varying inputs on neuron behavior.