worlov
- 20
- 0
In the essay „Über die Ablenkung des Lichtes I am Schwere*feld der Sonne“ ( http://adsabs.harvard.edu/full/1931ZA...3..171F ) the authors - Freundlich,
Klüber and Brunn - presented 1931 graphically the results of three expeditions, which took place 1919, 1922 and 1929. They put together all the measurements,
so that it gave a comprehensive presentation of 99 test points (illustration).
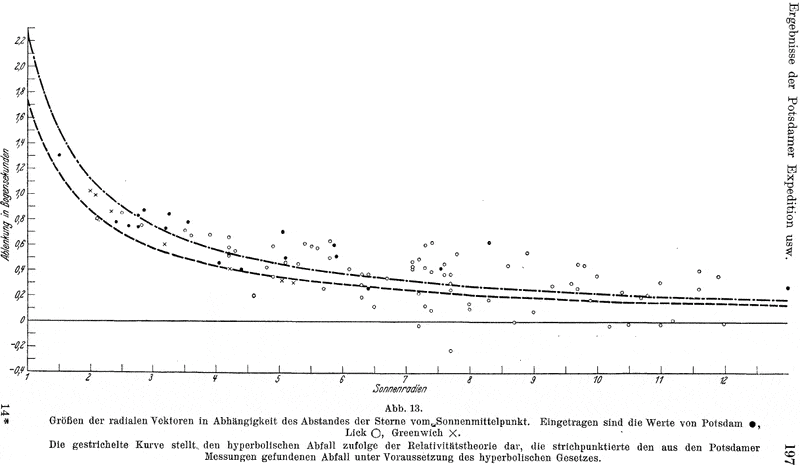
For the authors the theory of relativity is clearly failed: „It looks quite evident that the theoretical (lower) hyperbole is not represented by the values.“ Therefore,
they still draw the upper hyperbola for the light deflection at the solar limb by 2.24". The high quality of the image allows precise to determine the coordinates of
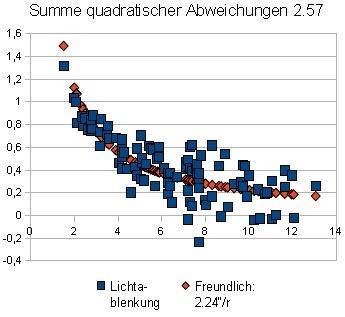
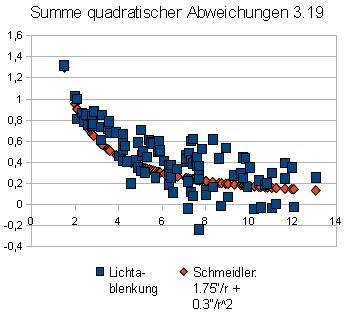
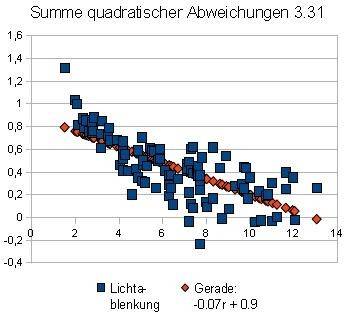
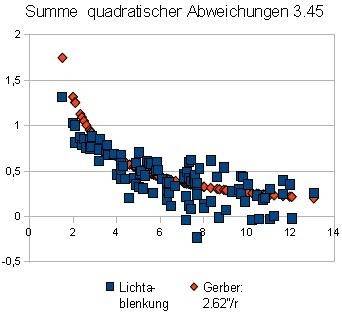
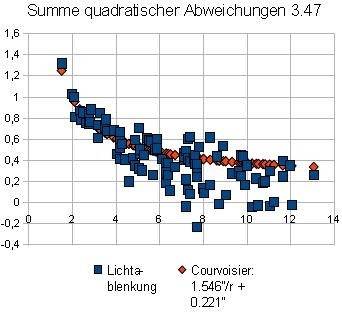
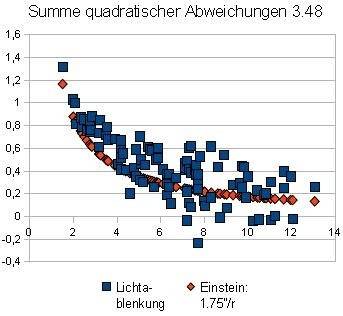
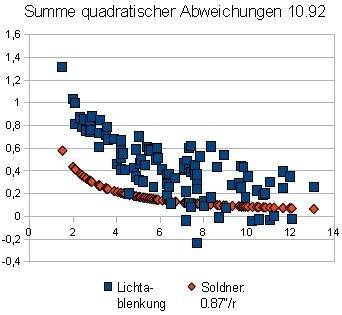
the measuring points. This data can for example be entered into the Excel spreadsheet and processed. In particular we are interested for the sum of squared
deviations between theoretical curves and real measurement values. The smaller it is, the better the compensation. The next charts are sorted by rise
of the sum, i.e. first get the best results.
And this as the table again:
Placement / Author / Equation / Type / Sum of squared deviations
-----------------------------------------------------------------------------------------
1. Freundlich / 2.24"/r / empirically / 2.57
2. Schmeidler 1.75"/r + 0.3"/r² / empirically / 3.19
3. A straight line / -0.07r + 0.9 / empirically / 3.31
4. Gerber / 2.62"/r / theoretically / 3.45
5. Courvoier / 1.546"/r + 0.221" / empirically / 3.47
6. Einstein / 1.75"/r / theoretically / 3.48
7. Soldner / 0.87"/r / theoretically / 10.92
Klüber and Brunn - presented 1931 graphically the results of three expeditions, which took place 1919, 1922 and 1929. They put together all the measurements,
so that it gave a comprehensive presentation of 99 test points (illustration).
For the authors the theory of relativity is clearly failed: „It looks quite evident that the theoretical (lower) hyperbole is not represented by the values.“ Therefore,
they still draw the upper hyperbola for the light deflection at the solar limb by 2.24". The high quality of the image allows precise to determine the coordinates of
the measuring points. This data can for example be entered into the Excel spreadsheet and processed. In particular we are interested for the sum of squared
deviations between theoretical curves and real measurement values. The smaller it is, the better the compensation. The next charts are sorted by rise
of the sum, i.e. first get the best results.
And this as the table again:
Placement / Author / Equation / Type / Sum of squared deviations
-----------------------------------------------------------------------------------------
1. Freundlich / 2.24"/r / empirically / 2.57
2. Schmeidler 1.75"/r + 0.3"/r² / empirically / 3.19
3. A straight line / -0.07r + 0.9 / empirically / 3.31
4. Gerber / 2.62"/r / theoretically / 3.45
5. Courvoier / 1.546"/r + 0.221" / empirically / 3.47
6. Einstein / 1.75"/r / theoretically / 3.48
7. Soldner / 0.87"/r / theoretically / 10.92