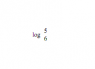Log Question - Relationship between two points on log function

[maplesyrup23]

Hi Physics Forums,

I understand that I usually need to show that I've attempted a question in order to get feedback, but I have absolutely no idea how to approach this one Calculus Log question.

Base = 10

log (2) = 0.301103, log (3) = 0.47715

a.) Find log base 6 (5)

b.) Estimate the number of digits in 15^10

I'd appreciate being pointed in the right direction.

 

[TylerH]

Are you sure it isn't log base 5 of 6? Question a is impossible to do with the information given.

As for b, think of log base 10 and how numbers are written in base 10. Like, for example, 145 = 1*10^2 + 4*10^1 + 5*10^0. Since you know that a*10^1 + b^10^0, where a and b are between 0 and 9 inclusive, will never sum with c*10^2 to make a number higher than 999. log base 10 of any number between 100 and 999 will truncate to 2. Likewise, the log of any number between 1000 to 9999 will truncate down to 3. See the pattern?

 

[maplesyrup23]

Are you sure it isn't log base 5 of 6? Question a is impossible to do with the information given.

It is possible I am reading it wrong, I haven't seen it written like this before, look at the printscreen.

EDIT: Sorry about the size of the image.

 

[TylerH]

That's definitely log base 6 of 5. There may be a way to do it, but if there is, I don't know it.

 

[maplesyrup23]

That's definitely log base 6 of 5. There may be a way to do it, but if there is, I don't know it.

Crap, thanks anyways.

 

[lurflurf]

Are you sure it isn't log base 5 of 6? Question a is impossible to do with the information given.

That is not true.

recall logb(xy)=logb(x)+logb(y)
a.) Find log base 6 (5)
log6(5)=log10(5)/log10(6)

recall logb(x^y)=y*logb(x)
b.) Estimate the number of digits in 15^10
digits~log10(15^10)

 

[TylerH]

I assumed it was to be done with the log10 of 2 and 3. To clarify, it is impossible to estimate log6(5) with log10(2) and log10(3), using algebraic means.

 

[maplesyrup23]

That is not true.

recall logb(xy)=logb(x)+logb(y)
a.) Find log base 6 (5)
log6(5)=log10(5)/log10(6)

recall logb(x^y)=y*logb(x)
b.) Estimate the number of digits in 15^10
digits~log10(15^10)

yeah Tyler was right. You're supposed to be using the given log values in the OP to do this question.

log 3 = 0.477,
and log 2 = 0.301

 

[lurflurf]

^No. Tyler said the given log values could not be used to do this question, but they can.

Try to rewrite each desired log ie log10(6), log10(5), log10(15) in terms of the given logs log10(2) = 0.301103, log10(3) = 0.47715, log10(10)=1 by using the familar rules
logb(xy)=logb(x)+logb(y)
logb(x/y)=logb(x)-logb(y)
logb(x^y)=y*logb(x)

 

[TylerH]

log10(6) is trivial. But how, exactly, do you get 5 by multiply or dividing 2 and 3? Once you have log10(5) with whatever method you decide to use, log10(15) also becomes trivial. The problem is log10(5), you're never going to find a way to get log10(5) with the given the information.

 

[lurflurf]

I am not being a smart ***, you will benifit more if you try to do your own assignment.
You should know that log10(10)=1, which I reminded you of above, from which
log10(5)=log10(10/2)=log10(10)-log10(2)=1.000000-0.301103

 

[TylerH]

You should know its not my assignment.

I'll concede, I didn't see that way.