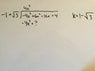FritoTaco
- 132
- 23
NO TEMPLATE BECAUSE MOVED FROM ANOTHER FORUM
Hello,
I've been trying to figure out how it works for complicated problems, I know how to use long division, but I'm not understanding how this process is done for a problem like I have.
Instructions: Write the function in the form ƒ(x) = (x - k)q(x) + r for the given value of k, and demonstrate that ƒ(k) = r
Problem: ƒ(x) = -4x³ + 6x² + 4,
My Work: So as you can see from my first attached file, I knew that if I wanted to cancel out 4x³ in the dividend, I would multiply 4x³ on top (quotient) with -1 (divisor). But I also now have to multiply 4x³ with √3. I don't know how to answer it? That's where my question mark is.
In my second attachment, you can see I put what I think is right. Then I drop down the 6x² because that's what you do in long division. So the 4x³ cancels out, but then I have two different degrees in the next part. I don't think I can do anything with that.
Another thing is that you've probably read the "Remainder Theorem in the question, I've already done that here so that's fine. I get a remainder of 0. This is the remainder I should get when I long divide.
Remainder Theorem
ƒ(1 - √3) = -4(1 - √3)³ + 6(1 - √3)² + 12(1 - √3) + 4
Solve: equals 0, so remainder is 0.
Then, for the answer, it's asking to put into form of, ƒ(x) = (x - k)q(x) + r. I already have (x - k) which is the (-1 + √3), I would multiply that with q(x), which is what I'm stuck on for getting the quotient in long division. Lastly, I would add the remainder (r) which there is none.
Hello,
I've been trying to figure out how it works for complicated problems, I know how to use long division, but I'm not understanding how this process is done for a problem like I have.
Instructions: Write the function in the form ƒ(x) = (x - k)q(x) + r for the given value of k, and demonstrate that ƒ(k) = r
Problem: ƒ(x) = -4x³ + 6x² + 4,
k = 1 - √3 <--- when plugging in q in divisor, signs change as you can see in my picture.
My Work: So as you can see from my first attached file, I knew that if I wanted to cancel out 4x³ in the dividend, I would multiply 4x³ on top (quotient) with -1 (divisor). But I also now have to multiply 4x³ with √3. I don't know how to answer it? That's where my question mark is.
In my second attachment, you can see I put what I think is right. Then I drop down the 6x² because that's what you do in long division. So the 4x³ cancels out, but then I have two different degrees in the next part. I don't think I can do anything with that.
Another thing is that you've probably read the "Remainder Theorem in the question, I've already done that here so that's fine. I get a remainder of 0. This is the remainder I should get when I long divide.
Remainder Theorem
ƒ(1 - √3) = -4(1 - √3)³ + 6(1 - √3)² + 12(1 - √3) + 4
Solve: equals 0, so remainder is 0.
Then, for the answer, it's asking to put into form of, ƒ(x) = (x - k)q(x) + r. I already have (x - k) which is the (-1 + √3), I would multiply that with q(x), which is what I'm stuck on for getting the quotient in long division. Lastly, I would add the remainder (r) which there is none.
Attachments
Last edited by a moderator: