MATLAB - Motion of a body around a central one

[MMS]

Hello everyone,

I've written a code using ode45 which describes the motion of a body m around a central one M (e.g a satellite around earth). I've done it with initial values that set the trajectory of the particle to be elliptic.

Clearly, energy and angular momentum need be conserved in this and so I get. However, I'm looking to reduce the error as much as possible and get a more accurate solution.

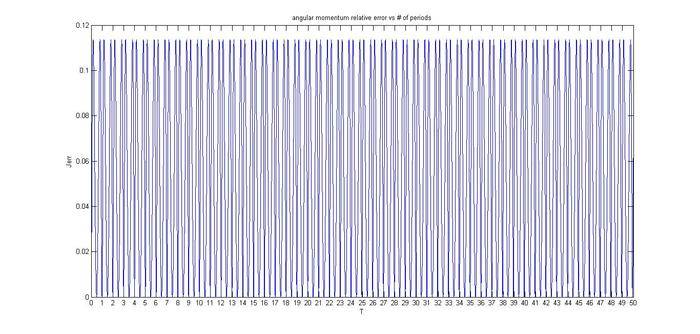
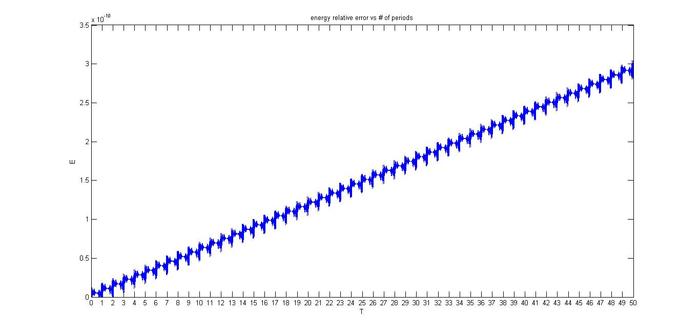
For the energy, I've managed to get a really small one using the relative and absolute tolerance. For example, for some parameters of RelTol and AbsTol, the relative error can reach a maximum value of about ~1e-8% only for 50 periods. However, the relative error in angular momentum doesn't seem to be affected by whatever I set the RelTol and AbsTol to be and the maximum value that it reaches (it is periodic, see the graph below) is constant at 11.36%.

I've already tried playing with the step size as well and it doesn't seem to affect it.

You can see two images below that describe the energy and angular momentum in 50 periods. The y-axis describes the relative error (not in percentage) in each parameter and the x-axis describes the number of periods (50 in this case).

Does anyone have any suggestion as to how to control and diminish the relative error in angular momentum?

Thanks in advance.

 

[MisterX]

I think that function uses the Runge-Kutta Method. The Runge-Kutta method is prone to energy error divergence at a long timescale when the true orbit should be periodic. The Verlet method allows bounded error in energy for periodic orbits. I am not sure if using Verlet instead would lead to better angular momentum error. I am not sure about the issue you are having with angular momentum error or how to improve it except smaller step size.

I am also wondering about ode solvers which might be able to enforce constraints like conserved energy somehow.

 

[MMS]

I think that function uses the Runge-Kutta Method. The Runge-Kutta method is prone to energy error divergence at a long timescale when the true orbit should be periodic. The Verlet method allows bounded error in energy for periodic orbits. I am not sure if using Verlet instead would lead to better angular momentum error. I am not sure about the issue you are having with angular momentum error or how to improve it except smaller step size.

I am also wondering about ode solvers which might be able to enforce constraints like conserved energy somehow.

It does use the Runge-Kutta method and you can see from the results that the error in energy is very small so I don't really have a problem with that.
However, the angular momentum stays the same regardless of the step size I take...