tactical
- 6
- 0
Hello,
I need help writing a MATLAB program to solve a heat transfer problem implicitly. For some reason this is very confusing to me. The problem is stated below. Any help is greatly appriciated. Let me know if you need a little more info.
I need to write a program to solve this problem. I want to solve for a temperature T(i,n) using the temperature at the 3 nodes ahead of it. Essentially it's going to be a tridiagonal matrix in which you can solve using Thomas Algorithm. I just need help writing a program to get this tridiagonal matrix.
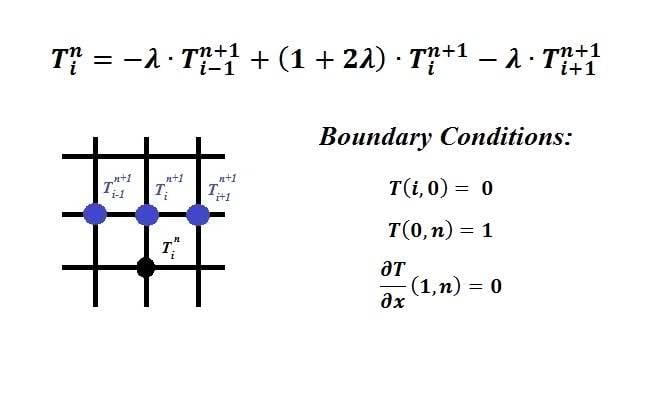
Edit: Also, all variable are dimensionless, therefore time goes from 0 to 1 and x also goes from 0 to 1. time is broken up into Δn parts and x is broken up into Δi parts. λ = Δt/Δx2
I need help writing a MATLAB program to solve a heat transfer problem implicitly. For some reason this is very confusing to me. The problem is stated below. Any help is greatly appriciated. Let me know if you need a little more info.
I need to write a program to solve this problem. I want to solve for a temperature T(i,n) using the temperature at the 3 nodes ahead of it. Essentially it's going to be a tridiagonal matrix in which you can solve using Thomas Algorithm. I just need help writing a program to get this tridiagonal matrix.
Edit: Also, all variable are dimensionless, therefore time goes from 0 to 1 and x also goes from 0 to 1. time is broken up into Δn parts and x is broken up into Δi parts. λ = Δt/Δx2