Discussion Overview
The discussion revolves around solving a transportation problem for the BFE company, which involves optimizing the distribution of financial calculators produced at three plants to four wholesalers. Participants explore the formulation of the problem, including decision variables, objective functions, and constraints, with a focus on maximizing profit.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Homework-related
- Debate/contested
Main Points Raised
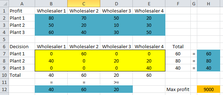
- Participants outline the production capacities of the plants and the commitments to the wholesalers, emphasizing the need to determine how many units to ship to wholesalers 3 and 4.
- Some participants propose a linear optimization approach, identifying decision variables, the objective function, and constraints necessary for maximizing profit.
- One participant presents a mathematical formulation for the problem, including a proposed objective function and constraints, and seeks validation of their approach.
- There is a discussion about the redundancy of a constraint related to wholesaler 4, with some participants questioning its necessity.
- Several participants express confusion about the steps to find the optimal solution, with requests for clarification on both Excel methods and manual calculations.
- One participant suggests that the amount sold to wholesaler 4 should be maximized, while another participant questions the formulation of a constraint that implies it should be zero.
Areas of Agreement / Disagreement
Participants generally agree on the need to maximize profit through optimization but express differing views on specific constraints and the formulation of the problem. The discussion remains unresolved regarding the optimal approach and the necessity of certain constraints.
Contextual Notes
There are limitations in the clarity of the problem statement, particularly regarding the constraints related to wholesaler 4. Participants also express uncertainty about the correct application of optimization techniques and the implications of their mathematical formulations.
Who May Find This Useful
This discussion may be useful for students or practitioners interested in linear optimization, transportation problems, and mathematical modeling in operational contexts.