Discussion Overview
The discussion revolves around a mechanics problem involving connected particles, specifically focusing on a system of pulleys and masses. Participants explore the relationships between the masses and the lengths of the rope and boxes involved in the setup.
Discussion Character
- Homework-related
- Mathematical reasoning
Main Points Raised
- One participant presents a problem involving two pulleys and three boxes, asking for the mass of the third box.
- Another participant suggests that the total length of the rope is 16 m and calculates the mass m to be 7.5 kg.
- A later reply corrects the previous claim, stating that the textbook answer is 6 kg, indicating a potential error in the trig ratio used.
- Several participants express confusion about the solution method and request clarification on how to solve the problem.
- One participant provides a mathematical approach involving a radical equation, leading to a solution for h and confirming it checks out.
- Another participant expresses gratitude for the clarification and notes a lack of explanation in the textbook regarding similar problems.
Areas of Agreement / Disagreement
There is no consensus on the correct mass of the third box, as participants propose different values (7.5 kg vs. 6 kg) and express confusion about the solution process. The discussion remains unresolved regarding the best approach to the problem.
Contextual Notes
Participants mention issues with understanding the problem and the methods used to solve it, indicating potential gaps in the textbook explanations and the need for further review of radical equations.
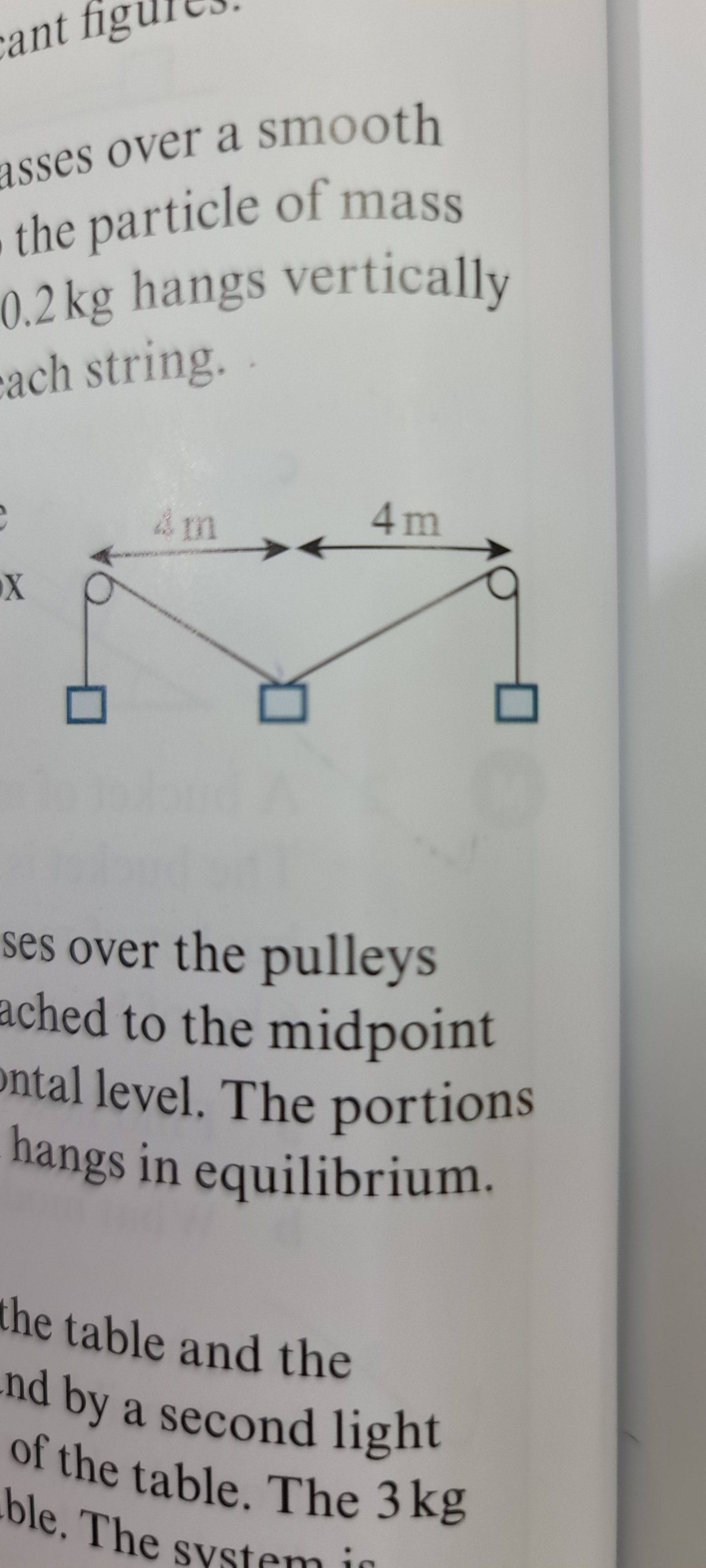 level. The total length of the box is 16m. Find the value of m
level. The total length of the box is 16m. Find the value of m