Min-Max over a closed bounded region

In summary, the function is \[f(x,y)=x^{2}+y^{2}-xy\] and the region is \[\left | x \right |+\left| y \right |\leq 1\]. The book claims that the maximum value is at (1,-1) and (-1,1) while the minimum is at (0.5,-1) and (-1,0.5). However, these points are not in the given region, leading to confusion and questioning the accuracy of the answer. The possibility of a mistake in the book or looking up the wrong answer is considered.
  • #1
Yankel
395
0
Hello again

I have another question regarding absolute min-max over a region. This is a weird one.

My function is:

\[f(x,y)=x^{2}+y^{2}-xy\]

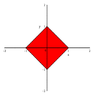
and the region is:

\[\left | x \right |+\left | y \right |\leq 1\]

Now, I have plotted the region using Maple:

View attachment 2601

The answer in the book where it came from is weird, it say that the maximum value is at the points: (1,-1) and (-1,1) while the minimum is at (0.5,-1) and (-1,0.5)

All these points are NOT in the region ! Am I missing something ?

My intuition say that these answers are for a different question.

Thanks !
 

Attachments

  • absolute value.PNG
    absolute value.PNG
    2.5 KB · Views: 65
Physics news on Phys.org
  • #2
There is certainly something wrong here. The answer bears no relation at all to the question. Either the book is wrong or you have looked up the answer to the wrong question. :p
 
  • #3
No, these answered were copied from a book, not by me, so the wrong answer was copied.

Just wanted to make sure, I thought I miss something very basic :D
 

FAQ: Min-Max over a closed bounded region

What is the concept of Min-Max over a closed bounded region?

The concept of Min-Max over a closed bounded region refers to finding the minimum and maximum values of a function over a specific region or interval. This is often used in optimization problems, where the goal is to find the optimal value of a variable within a given range.

How is the Min-Max over a closed bounded region calculated?

The Min-Max over a closed bounded region is typically calculated using calculus techniques such as differentiation and integration. The first step is to find the critical points of the function, which are the points where the derivative is equal to 0 or undefined. Then, the values at the critical points and the endpoints of the region are compared to determine the minimum and maximum values.

What is the difference between a closed and an open bounded region?

A closed bounded region is a finite interval that includes its endpoints, while an open bounded region is a finite interval that does not include its endpoints. In other words, a closed region has a defined maximum and minimum value, while an open region does not have defined maximum and minimum values.

What are some real-world applications of Min-Max over a closed bounded region?

Min-Max over a closed bounded region is commonly used in economics, engineering, and physics to optimize various parameters. For example, a company may use this concept to determine the optimal production level for maximum profit, or a bridge designer may use it to find the most cost-effective design for a given weight limit.

Are there any limitations to using Min-Max over a closed bounded region?

One limitation of using Min-Max over a closed bounded region is that it assumes the function is continuous and differentiable over the entire region. This may not always be the case in real-world scenarios, and alternative methods may need to be used. Additionally, this concept may not provide the most accurate solution if the function is highly complex or has multiple local minimum and maximum points.

Similar threads

MHB How to evaluate a double integral over a bounded region?
Replies
5
Views
2K
Find the global max/min for z=xy^2 - 5 on the region bounded by y=x
Replies
2
Views
2K
I Understanding a proof of inexistence of max nor min
Replies
4
Views
1K
MHB AP.6.1.1 A region is bounded between the graphs
Replies
3
Views
2K
MHB How Do You Find the Absolute Min and Max of a Function on a Triangular Region?
Replies
4
Views
2K
MHB Solve Optimization Problem: Find Min & Max of f(x,y)
Replies
3
Views
2K
B Why is this definite integral a single number?
Replies
20
Views
3K
MHB How Do You Calculate Volume by Rotating a Region Bounded by Curves?
Replies
9
Views
2K
MHB Find Absolute Extrema Over Region R
Replies
3
Views
5K
MHB Surface Integral of $F$ Over Region V
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top