Moving magnet and conductor - Residual worry

[Philip Wood]

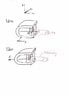
This is about a famous thought experiment, cited by Einstein at the beginning of his first 1905 paper on SR, and discussed in textbooks and on this forum. I've fleshed it out with a specific set up, shown in the thumbnail.

Seen in the S frame, a wire aligned in the y direction moves at speed v in the x-direction through a magnetic field B in the z direction. A charge q in the wire experiences a magnetic force qvB in the -y direction, so there is an emf qvBL / q = BvL in the wire.

Seen in the S' frame, moving to the right at speed v relative to the S frame, the wire is stationary and the magnet is moving to the left at speed v. Because the wire is stationary there are no magnetic forces on the charge carriers in it. But there must still be an emf: viewing from a different frame can't change what happens. The force on the charge carriers must therefore arise from an electric field, in this new frame.

And that's just what we know from Maxwell/Lorentz/Einstein theory: B_z transforms to give an E_y. But the transformation is
$$E'_y=-\gamma v B_z.$$
This means that in the S' frame the force on charge q is $qE'=-q \gamma v B$ in the y-direction. Transverse lengths are Lorentz-invariant, so the emf in the S' frame is presumably $- \gamma Lv B$.

It's that $\gamma$ that worries me. Is it really the case that the emf's are different according to the frame you're observing from? Oddly enough, I have no difficulty accepting that the forces are different!

 

[Jano L.]

This is interesting theoretical question. Is the integral

$$
\oint (\mathbf E + \mathbf v \times \mathbf B )\cdot d\mathbf s
$$

around the circuit Lorentz invariant? I did not do the calculations, but I expect that it is not.

"emf" is a notion that originated in non-relativistic theory for situations where bodies move with speed << speed of light. It is not clear that it should apply also to circuits with parts in relativistic motion. The difference in emf calculated in the two ways you described is very small for common velocities in motors or generators, probably even so small that it does not matter.

 

[Philip Wood]

Thank you for replying. I agree entirely. The question arose because I'm teaching e-m induction to a pre-university student. I started, as usual with a moving conductor, regarding the emf as arising from magnetic forces on the charge carriers, as these are translated along with the conductor. I then show that this can be cast into the form emf = -dPhi/dt. My next step would have been to point out that the latter still applies even if it's the magnet that moves and the conductor that is stationary...

 

[Jano L.]

What you write is true, but I am afraid this can confuse the student, as the first example with moving rod is actually very hard to analyze satisfactorily within macroscopic EM theory. I would rather talk about the Faraday experiment with moving magnet in and out of a coil, or two current-conducting coils one of which is moving; talk about induced electromotive force due to electric field and about the flux rule first. Student should also know difference between electromotive and ponderomotive force. Only then I would bring up the experiment with rod on rails - the magnetic field here plays two roles, both as electromotive force (pushes electrons), and as ponderomotive force (damps down motion of the rod).

 

[Jano L.]

Now that I read it, the last part of my previous post is written rather badly. What I meant is that the magnetic field both moves the current around somehow, and damps the motion of the rod somehow. Both these effects are hard to explain with elementary means. One can probably do this in microscopic theory, but that requires some good knowledge of the macroscopic theory, so I would rather not begin explainin E. & M. with this example.

 

[Philip Wood]

Well, one man's confusion is another man's richness. I would strongly defend the moving rod as an introduction to e-m induction, and make these points…

• The emf arises in a way the student can understand: magnetic (Bqv) forces on moving charges. [The student can learn later that not all induced emfs arise in this way.]

• With the rails and closed circuit it is then easy to cast emf = BLv into emf = dPhi/dt, rather than to introduce the last equation from nowhere.

• There is no need - if you think it confuses - to put the rod on rails in a closed circuit. Instead one can let charges redistribute (owing to the magnetic force) in the rod until the electric field forces due to the redistributed charges balance the magnetic forces. Then we have $q \frac {V}{L} = Bqv$ in which V is the open circuit pd.

• If you do have the rod on rails with a resistor completing the circuit you do indeed have a magnetic (BIL) force opposing the rod being moved through the field. Whatever closed-circuit set-up you use, you're always going to have to put work in.

• It's a positive advantage that in this case it's so easy to see how the work is put in - pushing the rod. It makes energy conservation and Lenz's Law so clear. Of course a wise teacher won't flood the student's mind with Bqv forces along the rod and Bqv (or BIL) forces at right angles to the rod in the same lesson...

 

[Jano L.]

I suppose there is no one best way to teach electromagnetism. Much depends on the level and whom you are teaching. I admit that "the rod on rails" example is the simplest case of the Faraday flux law and the formulae and results are easily remembered.

But be prepared for some hard questions - like "how can the energy of the person pushing the rod get into the electric current and heat, if magnetic force $q \mathbf u_k \times \mathbf B$ acting on the particles does no work? Should not the rod just accelerate and the magnetic force merely make the charged particles orbit in circles?" This leads to realization that surface of the metal rod and microscopic fields are important for validity of EMF = $BLv$. Explaining this and how exactly systematic electromotive force from the magnetic field happens does not seem to be easy. But this does not seem to be at the hear of the concept "EM induction".

On the other hand, in examples where the circuits are static and the EMF is due to change in external magnetic field, one can explain the current by presence of induced electric field (EM induction). The induced electric field can do work on charges and if the circuit is closed, integral of it along the circuit gives EMF easily and apparently, free of difficulties. No subtle issues with work here. The equation
$$
emf = \frac{d\Phi}{dt}
$$
for fixed circuit can be introduced as postulate based on experiments (as it was, Faraday and Maxwell did this). We have to do this eventually, however we begin, because it is an independent law that does not follow from the Lorentz force formula. Why not do this in the beginning?

The fact that the Lorentz force formula also leads to the same flux rule is interesting, but it covers different and much special case, which is moreover hard to explain satisfactorily. I would probably mention it after the Faraday law or as an independent experimental observation that waits for explanation in terms of what we already know.

In the end, it is important to discuss both and other examples, I just wanted to point out the difficulty with the magnetic EMF.

 

[Philip Wood]

Thank you for this interesting response. You raise important issues.

But be prepared for some hard questions - like "how can the energy of the person pushing the rod get into the electric current and heat, if magnetic force $q \mathbf u_k \times \mathbf B$ acting on the particles does no work?

This arises in other contexts, such as the mutual attraction of two current-carrying wires or coils. It may well have been met already in the learning programme, though one could argue that its resolution depends partly on understanding induced emfs!

Should not the rod just accelerate and the magnetic force merely make the charged particles orbit in circles?" This leads to realization that surface of the metal rod and microscopic fields are important for validity of EMF = $BLv$. Explaining this and how exactly systematic electromotive force from the magnetic field happens does not seem to be easy.

No, indeed. But again the difficulty may not be encountered here for the first time. The whole idea of electrons flowing under electric fields in conductors is tricky even before magnetic fields are introduced.

So I don't dismiss the difficulties you raise, but I don't think they disrail the teaching sequence which I've outlined – and which is clearly not to your taste!

 

[Philip Wood]

Come to think of it, I'm not at all sure that emfs induced in a stationary circuit are any more free of complications than conductors moving and cutting flux. Most textbooks ignore issues of confinement of free electrons in the wire, and of thermal motion of electrons (which is presumably modified by the presence of a magnetic field). There is usually an assumption, explicit or implicit, that for the purposes of macroscopic electromagnetism, microscopic effects average out to make the wire act like a pipe, with the electrons behaving as if as if they all had the same drift velocity along it.

 

[vanhees71]

The problem with teaching Faraday's Law is that people start with the more complicated integral equations instead of using the local Maxwell equations to begin with. They are Lorentz covariant, and it becomes clear from the very beginning that there is not an electric and a magnetic field but just one electromagnetic field, which has electric and magnetic components, that are observer dependent, i.e., dependent on the choice of the inertial frame, from which you observe the electromagnetic phenomena. Then it's also immediately clear that never ever can occur any discrepancies in this description, because Maxwell's equations are a fully Lorentz covariant theory. The electromagnetic field is represented by an antisymmetric 2nd-rank Minkowski tensor (Faraday tensor) and the charge and current density together build a Minkowski four-vector.

So the right way is to start with the Maxwell equations for the electromagnetic field in vacuo with all charge and current densities considered.

Then you can do classical electron theory and derive the usual simple constitutive relations for electrodynamics in media as linear-response approximation. Usually one gives the semi-Galilean version of this, and this gives rise to further trouble with Lorentz invariance, because it's clearly an approximation (which of course is usually totally sufficient for practical purposes). If you do the fully relativistic scheme, you get the Lorentz covariant constitutive relations first derived by Minkowski. Then also here no problem occurs.

Now to the example with the moving rod. You'll get the correct physics by using the correct integral laws derived from the local Maxwell equations. Then you'll find that indeed not the magnetic field does work on the electrons but the electric field driving the electrons through the circuit and the work you put in is changed into heat from the friction of the electrons due to collisions with the crystal lattice of the metal. It becomes clear from the microscopic derivation that electric conductivity is nothing else than a friction coefficient of the electrons.

The book that comes closest to this program of teaching electromagnetics is volume II of the Feynman Lectures, where this point of view is given at several places. Unfortunately it's not put everywhere to the very end. The reason is that the fully relativistic treatment is rarely really necessary (note that the electrons in the usual household currents are very slow even on our everyday scale of speeds, let alone compared to the speed of light) and leads to more complicated equations. Sometimes, however, the full relativistic point of view is necessary. The prime example for this is the famous Faraday homopolar generator, which is treated in Feynman's book in a very clear way. He has also more examples for situations that are puzzling when the relativistic point of view is neglected, and the non-relativistic approximations are no applicable although it seems as if nothing is moving with a velocity close to the speed of light :-).

 

[Philip Wood]

vanhees71. Many thanks. I can see exactly where you're coming from. There are practical difficulties, though, in carrying out this programme. In the UK we try - rightly or wrongly - to teach the basics of electromagnetism before university and well before students are capable of doing the maths needed to understand Maxwell's equations or Lorentz invariance. And, to be fair, I don't think students taught in this way have to 'unlearn' many misconceptions; instead Maxwell's equations and Lorentz invariance give huge unifying insights into phenomena already encountered.

 

[vanhees71]

Sure, this program is meant for the theoretical-physics lecture at the universities, not for introductory lectures or even at high schools. There, you shouldn't bother students with problems that are not understandable without relativity, and there's still plenty of material you can treat then!