P(t)=6t^4-5t^3+200t=1200 what is t if p is 175000?

[chiuda]

It is an equation to do with population growth it asks approximately when (t- time in years) will population(p) be 175 000

I honestly can't figure it out this is far as i get

p(t)=6t^4-5t^3+200t+12000
175000=6t^4-5t^3+200t+12000
0=6t^4-5t^3+200t-163000


I honestly don't know what to do i am lost, I'm sure its not that complicated but i just would love some help.

Thanks in advance!:)

 

[berkeman]

It is an equation to do with population growth it asks approximately when (t- time in years) will population(p) be 175 000

I honestly can't figure it out this is far as i get

p(t)=6t^4-5t^3+200t+12000
175000=6t^4-5t^3+200t+12000
0=6t^4-5t^3+200t-163000


I honestly don't know what to do i am lost, I'm sure its not that complicated but i just would love some help.

Thanks in advance!:)

Have you tried factoring the RHS of the last equation?

 

[LCKurtz]

It is an equation to do with population growth it asks approximately when (t- time in years) will population(p) be 175 000

I honestly can't figure it out this is far as i get

p(t)=6t^4-5t^3+200t+12000
175000=6t^4-5t^3+200t+12000
0=6t^4-5t^3+200t-163000


I honestly don't know what to do i am lost, I'm sure its not that complicated but i just would love some help.

Thanks in advance!:)

Have you tried factoring the RHS of the last equation?

I don't think it is going to factor nicely. Notice the question asks for approximately the value of $t$. I would suggest trying a graph for a first approximation, which may be good enough. Or it would give a starting point for Newton's method if they are studying that. But there is an integer value of $t$ that gives a very close answer.

 

[chiuda]

yes i didn't get any further after that though so i thought someone might be able to help out with the problem am having :)

 

[LCKurtz]

yes i didn't get any further after that though so i thought someone might be able to help out with the problem am having :)

Use the quote button so people know to whom you are replying.

 

[chiuda]

Use the quote button so people know to whom you are replying.

Alright. Were you saying that to solve for the approximate I would just keep subbing in numbers until I got aprox. 175000. If so this seems very inefficient, are their any concrete and less exhausting ways to get the answer?

 

[ehild]

You can apply an iterative method. Rearrange the equation:

t^4=\frac{163000+5t(t^2-40)}{6}, start with t₁=\sqrt[4]{163000} as first approximation and get the next as t_{k+1}=\sqrt[4]{\frac{163000+5t_k(t_k^2-40)}{6}}

ehild

(Edited)

 

[LCKurtz]

Alright. Were you saying that to solve for the approximate I would just keep subbing in numbers until I got aprox. 175000. If so this seems very inefficient, are their any concrete and less exhausting ways to get the answer?

I would think for a problem like this a graphing program or calculator or a web page that does graphs would be appropriate for starters. So, no, I wouldn't (and didn't) graph it by hand.

 

[ehild]

Here is a plot of 6t^4-5t^3+200t-163000.

ehild

 

[Vaedoris]

I'm not good at this, so could someone explain whether using Picard's method can get the solution fast enough?

 

[ehild]

What do you mean on Picard's method?

Try to apply the iteration in post #8

Start with y1=20: y2=13.5, y3=13.02, y4=13.00

ehild

 

[Ray Vickson]

It is an equation to do with population growth it asks approximately when (t- time in years) will population(p) be 175 000

I honestly can't figure it out this is far as i get

p(t)=6t^4-5t^3+200t+12000
175000=6t^4-5t^3+200t+12000
0=6t^4-5t^3+200t-163000I honestly don't know what to do i am lost, I'm sure its not that complicated but i just would love some help.

Thanks in advance!:)

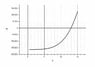
The question asks you for an approximate value, so a good way to go would be to plot p(t) and pick out where it equals 175,000. The exact solution to this problem is horrible: here is what Maple 14 gets for the smallest positive root of p(t) = 175000:

root =
5/24-1/24*((25*(414180+4380*5388398241^(1/2))^(1/3)-40*(414180+4380*5388398241^(1/2))^(2/3)
+18772800)/(414180+4380*5388398241^(1/2))^(1/3))^(1/2)
+ 1/24*10^(1/2)*((5*(414180+4380*5388398241^(1/2))^(1/3)*((25*(414180+4380*5388398241^(1/2))^(1/3)
-40*(414180+4380*5388398241^(1/2))^(2/3)+18772800)/(414180+4380*5388398241^(1/2))^(1/3))^(1/2)
+4*((25*(414180+4380*5388398241^(1/2))^(1/3)
-40*(414180+4380*5388398241^(1/2))^(2/3)+18772800)/(414180+4380*5388398241^(1/2))^(1/3))^(1/2)*(414180+4380*5388398241^(1/2))^(2/3)
-1877280*((25*(414180+4380*5388398241^(1/2))^(1/3)-40*(414180+4380*5388398241^(1/2))^(2/3)
+18772800)/(414180+4380*5388398241^(1/2))^(1/3))^(1/2)
+11495*(414180+4380*5388398241^(1/2))^(1/3))/(414180+4380*5388398241^(1/2))^(1/3)/((25*(414180+4380*5388398241^(1/2))^(1/3)
-40*(414180+4380*5388398241^(1/2))^(2/3)+18772800)/(414180+4380*5388398241^(1/2))^(1/3))^(1/2))^(1/2)
It is an irrational number. The other real root is a negative irrational, and there are also two complex conjugate irrational roots.

Nowadays we don't need to worry much about problems like this one because of ready availability of powerful computer methods. For example, if you have EXCEL you can get a numerical solution easily using the Solver tool. Many hand-held calculators would be able to do this problem with no difficulty. If all those tools are unavailable to you, you can still submit the problem to Wolfram Alpha, which costs you nothing if you already are paying for internet access.

RGV