Poles in Casimir force as function of frequency & mode

[Swamp Thing]

In Numerical methods for computing Casimir interactions, we have this expression for the Casimir force between two plates:

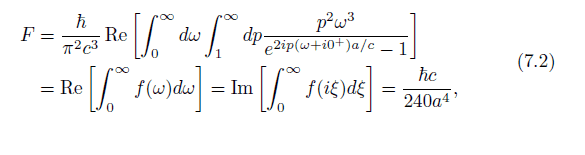
where

p is relatedto the plate-parallel momentum of the contributing modes/fluctuations.

I am trying to interpret this physically on a per-frequency and per-mode basis, before actually looking at the complete integral.

If we focus on a single frequency $\omega$, it seems that the force contribution as a function of the mode parameter $p$ can vary wildly and become arbitrarily large.

If we consider a narrow-band or even a single-frequency "excitation", the expression is telling us that certain modes will produce an infinite force. This infinite force would change sign abruptly from attractive to repulsive if we make small changes to $p$ or $\omega$ around those critical values.

How are we to interpret this physically? The authors focus more on how to tame this numerical headache, but not on why the force should behave this way.

 

[trurle]

I think this discontinuity happens because your integrals are not including boundary conditions for the edges of plates or finite conductivity of plates. Reference you cited seems specifically treat the perfect conductor. With infinite plate size and infinite conductivity no wonder certain (resonant) modes will have infinite quality factor and therefore eventually all zero-point energy between infinite perfectly conductive plates will convert to these modes, draining energy from non-resonant modes. This can be contradiction too - frequency conversion is generally lossy, therefore process which will allow "Casimir force resonance" as you described will likely introduce losses in form of (thermal) radiation.
Actually a^-4 law have the same power-law slope as radiative loss for electrically small antenna

 

[Swamp Thing]

Thank you!