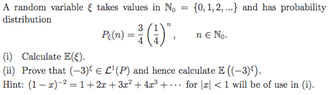SUMMARY
The discussion focuses on calculating expected values using a discrete probability distribution function (p.d.f.) defined as P{ξ = n} = (3/4)(1/4)ⁿ. The expected value E{ξ} is derived using the formula E{ξ} = (3/4)Σ(n(1/4)ⁿ), resulting in E{ξ} = 4/3. Additionally, the expected value E{(-3)ⁱ} is calculated as E{(-3)ⁱ} = (3/4)/(1 + 3/4) = 3/7. The conversation highlights a common confusion regarding the application of the series and the coefficients involved.
PREREQUISITES
- Understanding of discrete probability distributions
- Familiarity with expected value calculations
- Knowledge of summation series, particularly Σ(n xⁿ)
- Basic algebraic manipulation of fractions and series
NEXT STEPS
- Study the derivation of expected values in discrete probability distributions
- Learn about generating functions and their applications in probability
- Explore convergence of infinite series and their implications in statistics
- Investigate the properties of geometric series and their use in calculating expected values
USEFUL FOR
Students and professionals in statistics, data science, and mathematics who are working with discrete probability distributions and expected value calculations.